A Brief Introduction to Graph Convolutional Networks

This article was also inspired by my experience while writing paper notes and encountering graph convolutional networks.

The content became too lengthy, so I decided to write a separate article to introduce it.

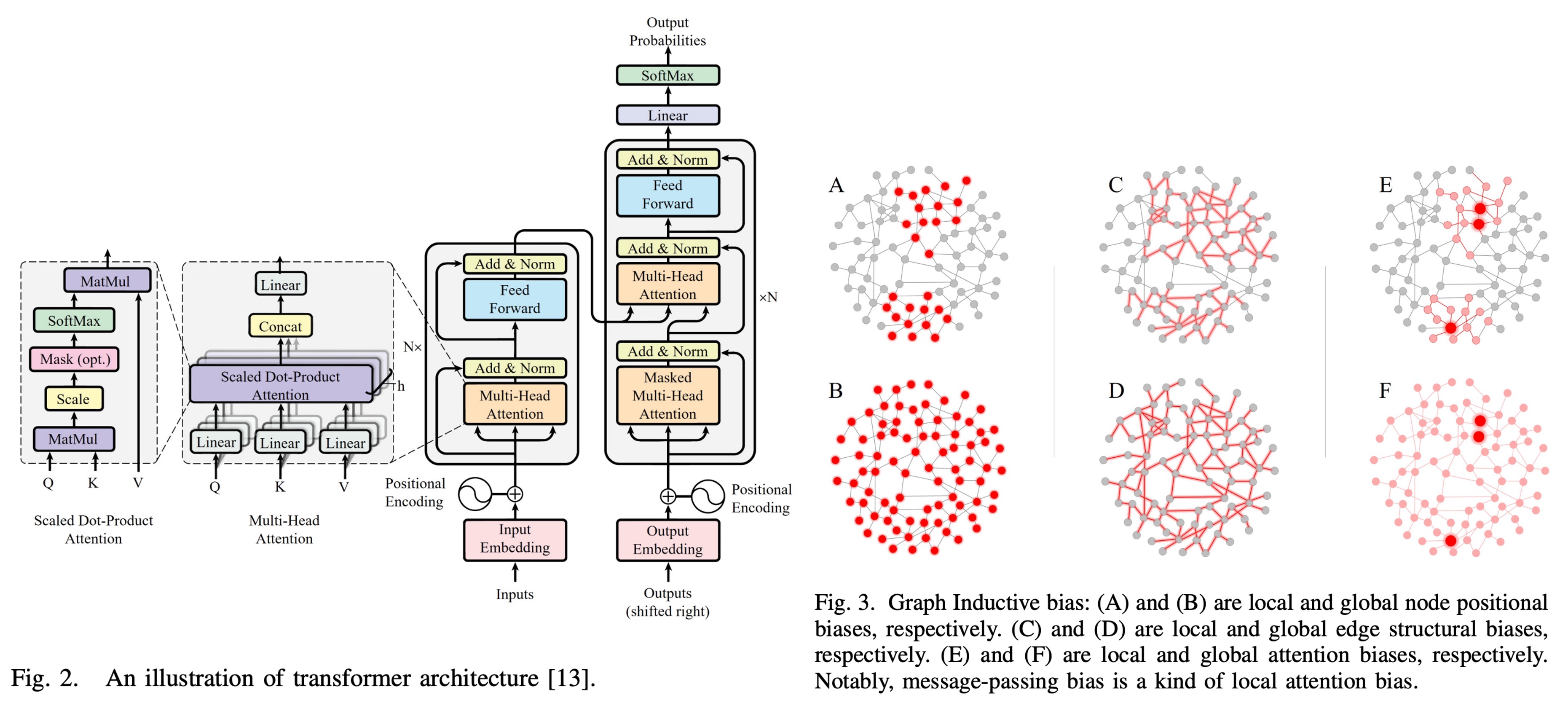
Thanks to OpenAI, everyone is now very familiar with Transformers. (Or at least, I hope so?)

Terms like self-attention mechanism, multi-head attention, and positional encoding are now household names.

So here, I’ll borrow the concept of Transformer to explain graph convolutional networks.

Graph Convolutional Networks​

Graph Convolutional Networks, abbreviated as GCN, is a model designed for deep learning on graph-structured data. Unlike traditional Convolutional Neural Networks (CNNs) which mainly deal with regular grid data (like images), GCN can process irregular graph-structured data. It is widely applied in fields such as social networks, knowledge graphs, and bioinformatics.

A graph consists of two basic elements:

1. Node: Represents entities in the data, such as people, items, or concepts.
2. Edge: Represents relationships between nodes, such as friendships or item similarities.

Each "node" has its own feature vector. For example, for a person, we might use features like height, weight, age, gender, and interests to describe them. These feature vectors form the "Feature Matrix". The "edges" are represented by the "Adjacency Matrix".

The adjacency matrix is used to describe the connection relationships between nodes in a graph. For a graph with $n$ nodes, the adjacency matrix $A$ is an $n \times n$ matrix where:

• $A_{ij} = 1$ indicates that there is an edge between node $i$ and node $j$.
• $A_{ij} = 0$ indicates that there is no edge between node $i$ and node $j$.

We’ll come back to compare Transformer and GCN later, but let’s continue exploring the basic concepts of GCN:

The properties and characteristics of the adjacency matrix are:

• Symmetry: If the graph is undirected, the adjacency matrix is symmetric, i.e., $A_{ij} = A_{ji}$.
• Self-connections: Some graphs allow nodes to have self-connections, i.e., $A_{ii} = 1$, but in most cases, this is set to $A_{ii} = 0$.

Example​

Let’s consider three people: Alice, Bob, and Carol, and their friendship relationships:

• Alice and Bob are friends.
• Bob and Carol are friends.
• Alice and Carol are not directly friends.

This relationship can be represented by the following adjacency matrix:

$$A = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}$$

In this matrix:

• $A_{12} = A_{21} = 1$: Indicates Alice and Bob are friends.
• $A_{23} = A_{32} = 1$: Indicates Bob and Carol are friends.
• All other elements are 0, meaning no direct friendship exists.

This adjacency matrix is "symmetric", so this graph is an "undirected graph".

If we visualize it, it would look like this:

Expanded Adjacency Matrix​

In practical applications, the adjacency matrix can be further expanded to represent additional information, such as:

1. Weighted Adjacency Matrix:

   If the strength of relationships between friends varies, we can use weight values to represent this. For example, if the number of interactions between Alice and Bob is 3, and the number of interactions between Bob and Carol is 5, the weighted adjacency matrix can be represented as:

   $$A = \begin{bmatrix} 0 & 3 & 0 \\ 3 & 0 & 5 \\ 0 & 5 & 0 \end{bmatrix}$$

2. Directed Adjacency Matrix:

   If the friendship relationships are directed (e.g., Alice contacts Bob first, but Bob does not contact Alice), the adjacency matrix becomes non-symmetric, like this:

   $$A = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}$$

   Here, $A_{12} = 1$ indicates that Alice contacted Bob first, while $A_{21} = 0$ shows that Bob did not contact Alice.

Feature Matrix​

In addition to the adjacency matrix, each node in the graph can also contain a feature vector, which together form the Feature Matrix $X$.

For a graph with $n$ nodes where each node has $d$-dimensional features, the feature matrix $X$ is an $n \times d$ matrix, where the $i$-th row represents the feature vector of node $i$.

Suppose each person has two features: age and exercise habits (represented by 1 for yes and 0 for no), we can construct the following feature matrix:

$$X = \begin{bmatrix} 35 & 1 \\ 50 & 0 \\ 22 & 1 \end{bmatrix}$$

This matrix can be interpreted as:

• The first row $[35, 1]$ represents Alice, who is 35 years old and has exercise habits.
• The second row $[50, 0]$ represents Bob, who is 50 years old and does not have exercise habits.
• The third row $[22, 1]$ represents Carol, who is 22 years old and has exercise habits.

We use the size of the circles to represent the nodes' ages, and the color to indicate whether they have exercise habits:

Mathematics of GCN​

After understanding the adjacency matrix and feature matrix, we can dive into the mathematical principles of Graph Convolutional Networks (GCN).

The core idea of GCN is to perform information propagation and aggregation on graph structures through the "convolution operation," in order to learn the representation (i.e., embedding vectors) of the nodes.

In traditional Convolutional Neural Networks (CNNs), the convolution operation mainly operates on the spatial structure of images, extracting features from local regions using convolutional filters. Similarly, GCN operates on the neighborhood structure of graphs, using information from neighboring nodes to update the feature representation of each node.

Each layer of a GCN can be seen as a message-passing mechanism, which primarily consists of the following steps:

1. Message Aggregation: Collect information from each node’s neighboring nodes.
2. Message Update: Combine the aggregated information with the node’s own features and update them via a nonlinear function.

The basic operation of GCN can be described by the following formula:

$$H^{(l+1)} = \sigma\left(\hat{A} H^{(l)} W^{(l)}\right)$$

Where:

• $H^{(l)}$ is the node feature matrix at the $l$-th layer. For the first layer, $H^{(0)} = X$, which is the input feature matrix.
• $W^{(l)}$ is the trainable weight matrix at the $l$-th layer.
• $\sigma$ is the nonlinear activation function, such as ReLU.
• $\hat{A}$ is the normalized adjacency matrix, used to stabilize training and account for the degree of nodes.

Using the original adjacency matrix $A$ directly for message passing could lead to excessively large or small eigenvalues, affecting the model’s stability.

Thus, we normalize the adjacency matrix as follows:

$$\hat{A} = \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2}$$

Where:

• $\tilde{A} = A + I_n$, and $I_n$ is the $n \times n$ identity matrix. This step is called adding self-loops, meaning each node is connected to itself.
• $\tilde{D}$ is the degree matrix of $\tilde{A}$, where the diagonal elements $\tilde{D}_{ii} = \sum_j \tilde{A}_{ij}$.

This normalization ensures that during message passing, the degree of nodes is taken into account, preventing certain nodes with overly high or low degrees from disproportionately affecting the overall learning process.

Let’s continue with the example mentioned earlier, where the adjacency matrix $A$ and feature matrix $X$ are as follows:

$$A = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}, \quad X = \begin{bmatrix} 35 & 1 \\ 50 & 0 \\ 22 & 1 \end{bmatrix}$$

• Step 1: Add Self-Loops

  First, we add self-loops to obtain $\tilde{A}$:

  $$\tilde{A} = A + I_3 = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix}$$

• Step 2: Calculate the Degree Matrix $\tilde{D}$

  $$\tilde{D} = \begin{bmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 2 \end{bmatrix}$$

• Step 3: Compute the Normalized Adjacency Matrix $\hat{A}$

  $$\hat{A} = \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix}$$

  The result of this calculation is:

  $$\hat{A} \approx \begin{bmatrix} 0.5 & \frac{1}{\sqrt{6}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{3} & \frac{1}{\sqrt{6}} \\ 0 & \frac{1}{\sqrt{6}} & 0.5 \end{bmatrix}$$

• Step 4: Apply the GCN Layer

  Suppose we have a GCN layer’s weight matrix $W^{(0)}$:

  $$W^{(0)} = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix}$$

  Then, the feature matrix $H^{(1)}$ for the next layer is:

  $$H^{(1)} = \sigma\left(\hat{A} X W^{(0)}\right)$$

  The specific computation steps are as follows:

  1. Matrix Multiplication: First, compute $\hat{A} X$:

     $$\hat{A} X \approx \begin{bmatrix} 0.5 & \frac{1}{\sqrt{6}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{3} & \frac{1}{\sqrt{6}} \\ 0 & \frac{1}{\sqrt{6}} & 0.5 \end{bmatrix} \begin{bmatrix} 35 & 1 \\ 50 & 0 \\ 22 & 1 \end{bmatrix} = \begin{bmatrix} 0.5 \times 35 + \frac{1}{\sqrt{6}} \times 50 + 0 \times 22 & 0.5 \times 1 + \frac{1}{\sqrt{6}} \times 0 + 0 \times 1 \\ \frac{1}{\sqrt{6}} \times 35 + \frac{1}{3} \times 50 + \frac{1}{\sqrt{6}} \times 22 & \frac{1}{\sqrt{6}} \times 1 + \frac{1}{3} \times 0 + \frac{1}{\sqrt{6}} \times 1 \\ 0 \times 35 + \frac{1}{\sqrt{6}} \times 50 + 0.5 \times 22 & 0 \times 1 + \frac{1}{\sqrt{6}} \times 0 + 0.5 \times 1 \end{bmatrix}$$

  2. Apply Weight Matrix $W^{(0)}$: Multiply the result by $W^{(0)}$.

  3. Apply Nonlinear Function $\sigma$: Typically, the ReLU function is used, i.e., $\sigma(x) = \max(0, x)$.

Through these steps, GCN is able to combine each node’s features with those of its neighbors, generating new feature representations.

This message-passing and aggregation mechanism enables GCN to capture both local and global information within graph structures, making it effective for a wide range of graph-related tasks such as node classification, graph classification, and link prediction.

In practice, multiple layers of GCN are often stacked to capture information from nodes at further distances. The output of each layer serves as the input for the next, allowing the model to progressively extract higher-level feature representations. For instance, a two-layer GCN enables each node’s representation to include information from its two-hop neighbors, while a three-layer GCN can incorporate information from three-hop neighbors, and so on.

GCN vs Transformer​

So, returning to the question we raised earlier:

Although the design intentions and application scenarios of Graph Neural Networks (GCNs) and Transformers are different, they share many core concepts, such as nodes, edges, and message passing and aggregation based on feature matrices. So what is the relationship between them?

• Can we view GCN as a special case of Transformer?

Let’s first review the core formulas of GCN and Transformer:

• Basic Update Formula of GCN

  $$H^{(l+1)} = \sigma\left(\hat{A} H^{(l)} W^{(l)}\right)$$

  Where:

  • $H^{(l)}$: Node feature matrix at layer $l$;
  • $\hat{A} = D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$: Weighted normalized adjacency matrix;
  • $W^{(l)}$: Learnable weight matrix at layer $l$;
  • $\sigma$: Nonlinear activation function.

  This formula aggregates local neighborhood information of nodes using the adjacency matrix $\hat{A}$, capturing both the structural information of the graph and the node features.

• Self-Attention Formula of Transformer

  $$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V$$

  Where:

  • $Q, K, V$: Query, Key, and Value matrices;
  • $d_k$: The dimension of the key vector;
  • $\text{softmax}$: Used for normalization, ensuring that the weights sum to 1.

  This formula enables the learning of global dependencies, with message aggregation depending on the dynamic calculation of similarity between features, independent of a fixed graph structure.

Restricted Attention Mechanism​

If we restrict the attention matrix of Transformer to the adjacency matrix of the graph (i.e., $\hat{A}$) and further assume that the attention weights are fixed (determined by the static structure of the graph), then the self-attention formula of Transformer simplifies to:

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V \rightarrow \text{softmax}(\hat{A}) V$$

Assuming that the query, key, and value matrices $Q, K, V$ all come from the same node feature matrix $H^{(l)}$, and that the weight matrices $W_Q = W_K = W_V = I$ (identity matrix), the formula becomes:

$$\text{Attention}(H^{(l)}, H^{(l)}, H^{(l)}) = \text{softmax}\left(\frac{H^{(l)} H^{(l)\top}}{\sqrt{d_k}}\right) H^{(l)}$$

If we further assume that $\text{softmax}\left(\frac{H^{(l)} H^{(l)\top}}{\sqrt{d_k}}\right) = \hat{A}$, i.e., the attention weights are fixed as the normalized adjacency matrix, then the self-attention formula simplifies to:

$$\text{Attention}(H^{(l)}, H^{(l)}, H^{(l)}) = \hat{A} H^{(l)}$$

At this point, the update formula for Transformer becomes:

$$H^{(l+1)} = \sigma\left(\hat{A} H^{(l)} W^{(l)}\right)$$

When comparing the two, in Transformer, the self-attention mechanism allows each node to interact with every other node in the graph, forming global dependencies. Mathematically, this is reflected in the attention weight matrix $\text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)$, which is a fully connected weight matrix, and the weights are dynamically calculated. In contrast, in GCN, message passing is limited to local neighborhoods, and the weight matrix $\hat{A}$ is sparse and fixed.

Differences in Weight Learning​

In Transformer, the attention weights are dynamically learned through the similarity between queries and keys, with the specific formula as follows:

$$\alpha_{ij} = \frac{\exp\left(\frac{Q_i K_j^\top}{\sqrt{d_k}}\right)}{\sum_{k} \exp\left(\frac{Q_i K_k^\top}{\sqrt{d_k}}\right)}$$

Where $\alpha_{ij}$ represents the attention weight from node $i$ to node $j$. This dynamic calculation allows the model to adaptively adjust the weights based on different input data, capturing complex relationships.

In contrast, in GCN, the weights are determined by the graph's adjacency structure, with the formula:

$$\hat{A}_{ij} = \frac{A_{ij}}{\sqrt{d_i d_j}}$$

Where $A_{ij}$ is an element of the adjacency matrix, indicating whether node $i$ and node $j$ are connected, and $d_i$ and $d_j$ are the degrees of nodes $i$ and $j$, respectively.

This fixed weight calculation limits the expressive power of the model but also reduces computational complexity.

Information Propagation Range and Efficiency​

In Transformer, information can propagate across the entire graph, which is mathematically reflected as a fully connected attention matrix. The computational complexity is $O(N^2)$, where $N$ is the number of nodes. This makes Transformer potentially face computational bottlenecks when dealing with large graphs.

In contrast, the message passing in GCN is limited to local neighborhoods, and the weight matrix $\hat{A}$ is sparse, with computational complexity typically being $O(N \cdot d)$, where $d$ is the average degree of nodes. This makes GCN more efficient for large-scale graph processing.

---

Therefore, from the perspective of formula simplification:

1. Attention matrix restricted to the graph’s adjacency matrix $\hat{A}$: The original self-attention mechanism in Transformer allows message passing between any two nodes, while GCN limits it to local neighborhoods within the graph. This restriction means that the range of message passing is determined by the graph's structure, rather than being dynamically learned.

2. Attention weights are fixed: In Transformer, self-attention weights are dynamically computed based on the similarity between queries and keys. If these weights are fixed as $\hat{A}$, i.e., no longer relying on the similarity between node features but entirely dependent on the static structure of the graph, the weights become non-learnable and fixed.

Given these two conditions, we believe GCN can indeed be considered a special case of Transformer.

Conclusion​

Graph Convolutional Networks (GCN) and Transformers have similarities and differences, each excelling in different areas.

In practical applications, they each have their advantages. For example, the self-attention mechanism in Transformer allows the model to dynamically adjust the weights of message passing based on data features, giving it an unparalleled advantage in handling complex and varied data patterns. On the other hand, while the fixed weights in GCN work excellently for some structured data, they are more limited in scenarios requiring dynamic relationships.

Furthermore, GCN is more suitable for handling data with clear graph structures, such as social network analysis, knowledge graphs, and recommendation systems, efficiently utilizing topological information. Transformer, however, performs excellently in domains such as natural language processing and computer vision, where sequential or high-dimensional data is handled, capturing long-range dependencies and complex patterns.

The topic of GCN is vast, with various variants and applications, and we’ve only introduced the basic concepts here.

We hope this article has helped you understand some of the fundamental principles and applications of GCN.

Interested in learning more about the latest applications of GCN and Transformer? Let’s take a look at the paper!

• [24.07] Graph Transformers: A Survey

  

References​

• [16.09] Semi-Supervised Classification with Graph Convolutional Networks
• [17.06] Attention is All You Need