淺談圖卷積網路

這篇文章也是因為在撰寫論文筆記時遇到了圖卷積網路。

篇幅實在太長了，只好單獨寫一篇來介紹一下。

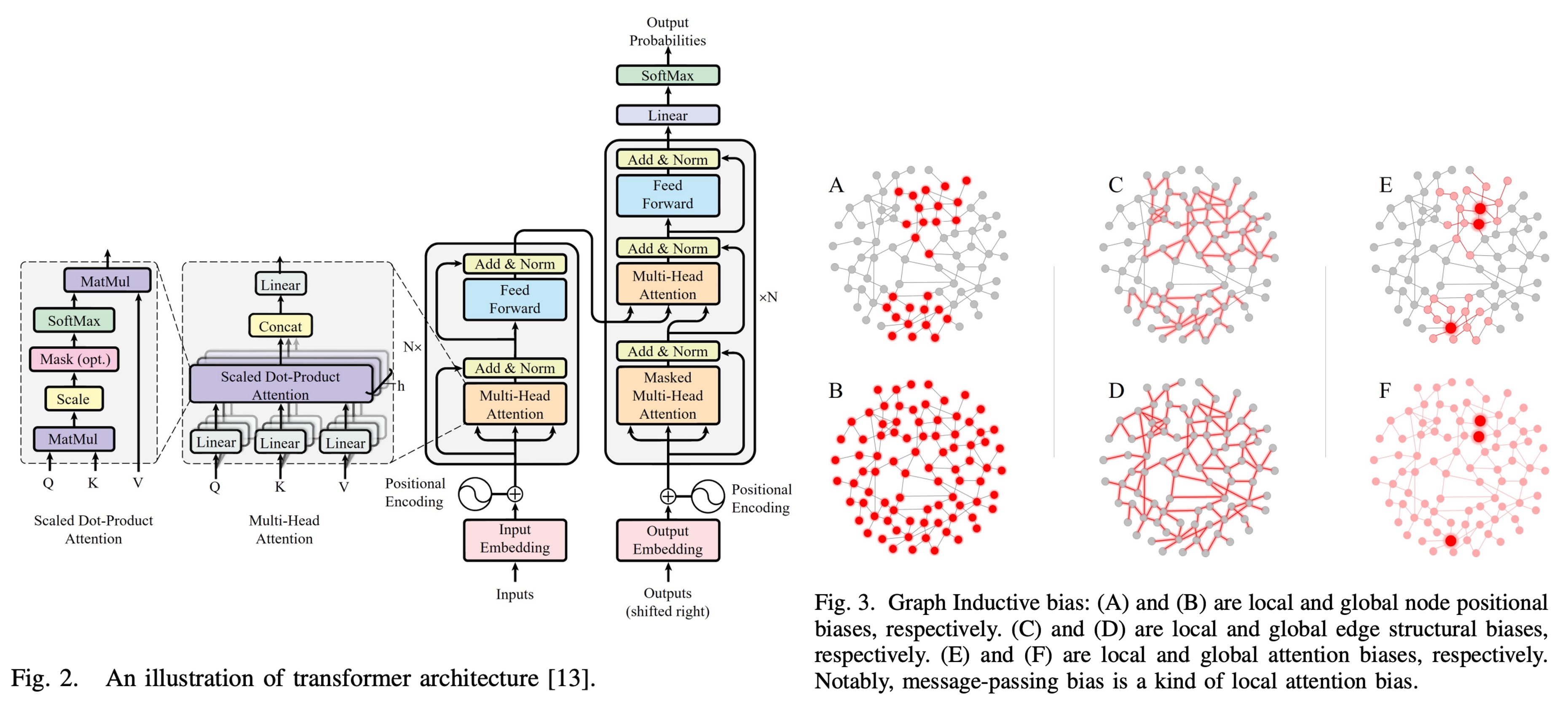
拜 OpenAI 所賜，現在大家對 Transformer 非常熟悉。（應該吧？）

各種自注意力機制、多頭注意力機制、位置編碼等等，都是大家耳熟能詳的名詞。

所以在這裡借用一下 Transformer 的概念來解釋一下圖卷積網路。

圖卷積網路​

圖卷積網路，原文為 Graph Convolutional Networks，又簡稱為 GCN。

它是一種在圖結構數據上進行深度學習的模型。與傳統的卷積神經網路（CNN）主要應用於規則網格數據（如圖像）不同，GCN 能夠處理不規則的圖結構數據，廣泛應用於社交網路、知識圖譜、生物信息學等領域。

圖的定義有兩個基本元素：

1. 節點（Node）：代表數據中的實體，如人、物品或概念。
2. 邊（Edge）：表示節點之間的關係，如朋友關係或物品相似性。

每個「節點」帶有各自的特徵向量，例如一個人，我們就會用身高、體重、年齡、性別、興趣等特徵來描述，這些特徵向量組成了「特徵矩陣（Feature Matrix）」。而「邊」的描述則是用「鄰接矩陣（Adjacency Matrix）」來表示。

鄰接矩陣是用來描述圖中節點之間連接關係的矩陣，對於一個有 $n$ 個節點的圖，鄰接矩陣 $A$ 是一個 $n \times n$ 的矩陣，其中：

• $A_{ij} = 1$ 表示節點 $i$ 和節點 $j$ 之間存在一條邊。
• $A_{ij} = 0$ 表示節點 $i$ 和節點 $j$ 之間不存在邊。

我們等一下再回來討論 Transformer 和 GCN 之間的對比，先繼續介紹 GCN 的基本概念：

鄰接矩陣性質與特點有：

• 對稱性：如果圖是無向圖，則鄰接矩陣是對稱的，即 $A_{ij} = A_{ji}$。
• 自連接：有些圖允許節點自連接，即 $A_{ii} = 1$，但在大多數情況下，通常設定為 $A_{ii} = 0$。

舉個例子​

假設有三個人：Alice、Bob 和 Carol，他們的朋友關係如下：

• Alice 和 Bob 是朋友。
• Bob 和 Carol 是朋友。
• Alice 和 Carol 之間沒有直接的朋友關係。

這個關係可以表示為以下的鄰接矩陣：

$$A = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}$$

在這個矩陣中：

• $A_{12} = A_{21} = 1$：表示 Alice 和 Bob 是朋友。
• $A_{23} = A_{32} = 1$：表示 Bob 和 Carol 是朋友。
• 其他元素為 0，表示沒有直接的朋友關係。

這個鄰接矩陣是「對稱的」，因此這個圖是一個「無向圖」。

轉成圖像的話，會長這樣：

擴展鄰接矩陣​

在實際應用中，鄰接矩陣還可以進一步擴展來表示更多信息，例如：

1. 加權鄰接矩陣：

   如果朋友之間的關係強弱不同，我們可以用權重值來表示。例如，Alice 和 Bob 之間的互動次數為 3，Bob 和 Carol 之間的互動次數為 5，那麼加權鄰接矩陣可以表示為：

   $$A = \begin{bmatrix} 0 & 3 & 0 \\ 3 & 0 & 5 \\ 0 & 5 & 0 \end{bmatrix}$$

2. 有向鄰接矩陣：

   如果朋友關係是有方向的（例如，Alice 主動聯繫 Bob，但 Bob 不主動聯繫 Alice），則鄰接矩陣會變為非對稱矩陣，例如：

   $$A = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}$$

   這裡 $A_{12} = 1$ 表示 Alice 主動聯繫了 Bob，而 $A_{21} = 0$ 表示 Bob 沒有主動聯繫 Alice。

特徵矩陣​

除了鄰接矩陣，圖中的每個節點還可以包含一組特徵向量，這些特徵組成了特徵矩陣（Feature Matrix） $X$。

對於一個有 $n$ 個節點且每個節點有 $d$ 維特徵的圖，特徵矩陣 $X$ 是一個 $n \times d$ 的矩陣，其中第 $i$ 行表示節點 $i$ 的特徵向量。

假設每個人有兩個特徵：年齡和運動習慣（用 1 表示有，0 表示沒有），我們可以構造如下的特徵矩陣：

$$X = \begin{bmatrix} 35 & 1 \\ 50 & 0 \\ 22 & 1 \end{bmatrix}$$

這裡的矩陣可以解讀為：

• 第一行 $[35, 1]$ 表示 Alice 年齡為 35 歲，有運動習慣。
• 第二行 $[50, 0]$ 表示 Bob 年齡為 50 歲，沒有運動習慣。
• 第三行 $[22, 1]$ 表示 Carol 年齡為 22 歲，有運動習慣。

我們用圓的大小來表示節點的年齡，用顏色來表示是否有運動習慣：

GCN 的數學​

在了解了鄰接矩陣和特徵矩陣之後，我們可以深入探討圖卷積網路（GCN）的數學原理。

GCN 的核心思想是通過「卷積操作」在圖結構上進行資訊的傳遞和聚合，從而學習節點的表示（即嵌入向量）。

在傳統的卷積神經網路（CNN）中，卷積操作主要在圖像的空間結構上進行，利用卷積核在局部區域內提取特徵。同樣的，GCN 在圖的鄰域結構上進行操作，利用鄰接節點的信息來更新每個節點的特徵表示。

GCN 的每一層可以被視為一個訊息傳遞機制，其主要步驟包括：

1. 訊息聚合（Aggregation）：從每個節點的鄰居節點收集資訊。
2. 訊息更新（Update）：將聚合到的資訊與自身特徵結合，通過非線性函數進行更新。

GCN 的基本操作可以用以下公式來描述：

$$H^{(l+1)} = \sigma\left(\hat{A} H^{(l)} W^{(l)}\right)$$

其中：

• $H^{(l)}$ 是第 $l$ 層的節點特徵矩陣。對於第一層，$H^{(0)} = X$，即輸入的特徵矩陣。
• $W^{(l)}$ 是第 $l$ 層的可訓練權重矩陣。
• $\sigma$ 是非線性激活函數，如 ReLU。
• $\hat{A}$ 是歸一化後的鄰接矩陣，用於穩定訓練並考慮到節點的度（degree）。

直接使用原始的鄰接矩陣 $A$ 進行訊息傳遞可能導致特徵值過大或過小，影響模型的穩定性。

為此，我們對鄰接矩陣進行歸一化處理：

$$\hat{A} = \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2}$$

其中：

• $\tilde{A} = A + I_n$，$I_n$ 是 $n \times n$ 的單位矩陣，這一步稱為添加自連接，即每個節點與自身相連。
• $\tilde{D}$ 是 $\tilde{A}$ 的度矩陣，對角線元素 $\tilde{D}_{ii} = \sum_j \tilde{A}_{ij}$。

這樣的歸一化確保了訊息傳遞時考慮到節點的度，避免某些節點因為度數過高或過低而影響整體學習效果。

我們繼續沿用上面提到的例子，鄰接矩陣 $A$ 和特徵矩陣 $X$ 的資訊如下：

$$A = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}, \quad X = \begin{bmatrix} 35 & 1 \\ 50 & 0 \\ 22 & 1 \end{bmatrix}$$

• 步驟 1：添加自連接

  首先，我們添加自連接，得到 $\tilde{A}$：

  $$\tilde{A} = A + I_3 = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix}$$

• 步驟 2：計算度矩陣 $\tilde{D}$

  $$\tilde{D} = \begin{bmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 2 \end{bmatrix}$$

• 步驟 3：計算歸一化鄰接矩陣 $\hat{A}$

  $$\hat{A} = \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & \frac{1}{\sqrt{3}} & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix}$$

  計算結果為：

  $$\hat{A} \approx \begin{bmatrix} 0.5 & \frac{1}{\sqrt{6}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{3} & \frac{1}{\sqrt{6}} \\ 0 & \frac{1}{\sqrt{6}} & 0.5 \end{bmatrix}$$

• 步驟 4：應用 GCN 層

  假設我們有一個 GCN 層的權重矩陣 $W^{(0)}$：

  $$W^{(0)} = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix}$$

  則下一層的特徵矩陣 $H^{(1)}$ 為：

  $$H^{(1)} = \sigma\left(\hat{A} X W^{(0)}\right)$$

  具體計算過程如下：

  1. 矩陣乘法：首先計算 $\hat{A} X$：

     $$\hat{A} X \approx \begin{bmatrix} 0.5 & \frac{1}{\sqrt{6}} & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{3} & \frac{1}{\sqrt{6}} \\ 0 & \frac{1}{\sqrt{6}} & 0.5 \end{bmatrix} \begin{bmatrix} 35 & 1 \\ 50 & 0 \\ 22 & 1 \end{bmatrix} = \begin{bmatrix} 0.5 \times 35 + \frac{1}{\sqrt{6}} \times 50 + 0 \times 22 & 0.5 \times 1 + \frac{1}{\sqrt{6}} \times 0 + 0 \times 1 \\ \frac{1}{\sqrt{6}} \times 35 + \frac{1}{3} \times 50 + \frac{1}{\sqrt{6}} \times 22 & \frac{1}{\sqrt{6}} \times 1 + \frac{1}{3} \times 0 + \frac{1}{\sqrt{6}} \times 1 \\ 0 \times 35 + \frac{1}{\sqrt{6}} \times 50 + 0.5 \times 22 & 0 \times 1 + \frac{1}{\sqrt{6}} \times 0 + 0.5 \times 1 \end{bmatrix}$$

  2. 應用權重矩陣 $W^{(0)}$：將結果與 $W^{(0)}$ 相乘。

  3. 應用非線性函數 $\sigma$：通常使用 ReLU 函數，即 $\sigma(x) = \max(0, x)$。

通過這幾個步驟，GCN 能夠將每個節點的特徵與其鄰居的特徵結合起來，生成新的特徵表示。

這種訊息傳遞和聚合的機制使得 GCN 能夠捕捉圖結構中的局部和全局信息，從而在各種圖相關的任務中表現出色，如節點分類、圖分類和鏈接預測等。

在實際應用中，通常會堆疊多層 GCN，以捕捉更遠範圍的節點信息。

我們把每一層的輸出作為下一層的輸入，如此可以逐層提取更高層次的特徵表示。例如兩層 GCN 可以讓每個節點的表示包含其兩跳鄰居的信息，三層 GCN 則可以包含三跳鄰居的信息，以此類推。

GCN vs Transformer​

所以，回到我們一開始提到的問題：

圖神經網路和 Transformer 雖然它們的設計初衷和應用場景有所不同，但它們共享許多核心概念，例如節點、邊以及基於特徵矩陣進行的訊息傳遞與聚合，所以它們之間有什麼關係呢？

• 我們可以視 GCN 為 Transformer 的一種特例嗎？

我們先回顧 GCN 和 Transformer 的核心公式：

• GCN 的基礎更新公式

  $$H^{(l+1)} = \sigma\left(\hat{A} H^{(l)} W^{(l)}\right)$$

  其中：

  • $H^{(l)}$：第 $l$ 層的節點特徵矩陣；
  • $\hat{A} = D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$：加權正則化的鄰接矩陣；
  • $W^{(l)}$：第 $l$ 層的可學習權重矩陣；
  • $\sigma$：非線性激活函數。

  此公式通過鄰接矩陣 $\hat{A}$ 將節點特徵進行局部鄰域訊息的加權聚合，捕捉圖的結構信息與節點特徵。

• Transformer 的自注意力機制公式

  $$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V$$

  其中：

  • $Q, K, V$ 分別是查詢（Query）、鍵（Key）、值（Value）矩陣；
  • $d_k$ 是鍵向量的維度；
  • $\text{softmax}$ 用於正則化，確保權重和為 1。

  該公式實現了全局依賴學習，訊息聚合依賴於特徵之間的相似性動態計算，與固定的圖結構無關。

受限的注意力機制​

若將 Transformer 的注意力矩陣限制於圖的鄰接矩陣（即 $\hat{A}$），並進一步假設注意力權重為固定值（由圖的靜態結構決定），則 Transformer 的自注意力公式可以簡化為：

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V \rightarrow \text{softmax}(\hat{A}) V$$

假設查詢、鍵和值矩陣 $Q, K, V$ 均來自相同的節點特徵矩陣 $H^{(l)}$，且權重矩陣 $W_Q = W_K = W_V = I$（單位矩陣），則公式變為：

$$\text{Attention}(H^{(l)}, H^{(l)}, H^{(l)}) = \text{softmax}\left(\frac{H^{(l)} H^{(l)\top}}{\sqrt{d_k}}\right) H^{(l)}$$

若進一步假設 $\text{softmax}\left(\frac{H^{(l)} H^{(l)\top}}{\sqrt{d_k}}\right) = \hat{A}$，即將注意力權重固定為經過正則化的鄰接矩陣，則自注意力公式簡化為：

$$\text{Attention}(H^{(l)}, H^{(l)}, H^{(l)}) = \hat{A} H^{(l)}$$

此時，Transformer 的更新公式變為：

$$H^{(l+1)} = \sigma\left(\hat{A} H^{(l)} W^{(l)}\right)$$

兩者對比之下，在 Transformer 中，自注意力機制允許每個節點與圖中所有其他節點進行訊息交互，形成全局依賴。這在數學上體現在注意力權重矩陣 $\text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)$ 是一個全連接的權重矩陣，且權重是動態計算的。而在 GCN 中，訊息傳遞僅限於局部鄰域，權重矩陣 $\hat{A}$ 是稀疏且固定的。

權重學習的差異​

在 Transformer 中，注意力權重是通過查詢和鍵的相似性動態學習的，具體的公式如下：

$$\alpha_{ij} = \frac{\exp\left(\frac{Q_i K_j^\top}{\sqrt{d_k}}\right)}{\sum_{k} \exp\left(\frac{Q_i K_k^\top}{\sqrt{d_k}}\right)}$$

其中 $\alpha_{ij}$ 表示節點 $i$ 對節點 $j$ 的注意力權重。這種動態計算允許模型根據不同的輸入數據自適應地調整權重，捕捉複雜的關聯性。

而在 GCN 中，權重由圖的鄰接結構決定，公式為：

$$\hat{A}_{ij} = \frac{A_{ij}}{\sqrt{d_i d_j}}$$

其中 $A_{ij}$ 是鄰接矩陣的元素，表示節點 $i$ 和節點 $j$ 是否相連，$d_i$ 和 $d_j$ 分別是節點 $i$ 和節點 $j$ 的度數。

這種固定的權重計算方式限制了模型的表達能力，但同時也降低了計算複雜度。

信息傳遞的範圍與效率​

在 Transformer 中，信息可以跨越整個圖進行傳遞，這在數學上體現為全連接的注意力矩陣，計算複雜度為 $O(N^2)$，其中 $N$ 是節點數量。這使得 Transformer 在處理大規模圖時可能面臨計算瓶頸。

相比之下，GCN 的訊息傳遞僅限於局部鄰域，權重矩陣 $\hat{A}$ 是稀疏的，計算複雜度通常為 $O(N \cdot d)$，其中 $d$ 是節點的平均度數，這使得 GCN 在處理大規模圖時更加高效。

---

因此，從公式簡化的角度看：

1. 注意力矩陣受限於圖的鄰接矩陣 $\hat{A}$： Transformer 原本的自注意力機制允許任意節點之間的訊息傳遞，而 GCN 則限制於圖的局部鄰域。這種限制意味著訊息傳遞範圍由圖的結構決定，而非動態學習。

2. 注意力權重為固定值： Transformer 的自注意力權重是動態計算的，基於查詢和鍵的相似性。如果將其固定為 $\hat{A}$，即不再依賴於節點特徵的相似性，而完全依賴於圖的靜態結構，則這些權重變得不再可學習，而是固定的。

我們認為，基於以上兩個條件，GCN 確實可以被視為 Transformer 的特例。

結論​

圖卷積網路和 Transformer 有點像又不太像，各擅勝場。

在實際應用中，他們有各自的優勢，像是 Transformer 的自注意力機制允許模型根據數據特徵動態調整訊息傳遞的權重，這使其在處理複雜和多變的數據模式時具有無可比擬的優勢。而 GCN 的固定權重雖然在某些結構化數據中表現出色，但在需要動態關聯性的場景中則相對受限。

此外，GCN 更加適合處理具有明確圖結構的數據，如社交網路分析、知識圖譜、推薦系統等，能夠高效地利用圖的拓撲信息。而 Transformer 則在自然語言處理、計算機視覺等需要處理序列或高維數據的領域中表現優異，能夠捕捉長距離依賴和複雜模式。

圖卷積網路的主題非常龐大，還有各種變種和應用，我們在這裡只是介紹了一個基礎的概念。

希望通過這篇文章，能夠幫助你理解一些基本的圖卷積網路的原理和應用。

想知道更多關於 GCN 和 Transformer 的最新應用嗎？一起來看論文吧！

• [24.07] Graph Transformers: A Survey

  

參考文獻​

• [16.09] Semi-Supervised Classification with Graph Convolutional Networks
• [17.06] Attention is All You Need