在寫論文筆記的時候遇到傅立葉轉換,想要講一下卻發現篇幅太長,喧賓奪主。
所以把這個章節獨立出來,簡單介紹一下相關知識。
大家小時候都有學過三角函數,應該都是三角函數大師。
三角函數在物理和工程領域中有著廣泛的應用,特別是在描述波動和振動方面。
波本質上是一種能量傳遞的方式,而這種傳遞通常以「週期性振動」的形式出現。
週期性?
比較常見的大概是鐘擺,它左右擺動的過程是一種週期性運動。當我們觀察它的運動軌跡時,可以發現它的位移會像波一樣變化,從正值變為零,再到負值,然後重複。
所以我們試著用三角函數來更精確的描述波,用數學表示為:
y(t)=Asin(2πft)
這裡的每個變數都與鐘擺運動有關:
- y(t):在時間 t 時,鐘擺的位移。
- A:振幅,表示鐘擺擺動的最大距離。
- f:頻率,表示鐘擺每秒擺動的次數。
有了正弦函數後,我們可以更精確地描述波的特性。
如果你仔細觀察,會發現有些波並非從零開始,而是偏移了一段時間才開始振動,這種偏移用「相位 ϕ」來表示。
完整的波形公式可以寫為:
y(t)=Asin(2πft+ϕ)
或是可以用餘弦函數表示:
y(t)=Acos(2πft+ϕ)
正弦波和餘弦波的差異在於相位的不同,它們都可以用來描述波的變化。
另外,為了更進一步描述波的變化速度,可以使用「角速度 ω」,它表示波每秒的相位變化量,公式為:
ω=2πf
為了方便觀察,我手寫了一個互動式圖表,你可以調整振幅、頻率和相位,觀察正弦波的變化。
有了正弦波和餘弦波,就像是有了 x 軸和 y 軸一樣的基本元素,可以通過疊加不同的波形來形成更複雜的波,例如:
y(t)=Acos(2πft)+Bsin(2πft)
上式中,A 和 B 是係數,決定了餘弦和正弦成分的大小,透過疊加多個波,可以形成複雜的波形。
你使用以下互動式圖表,調整兩個正弦波的參數,觀察它們疊加後的波形。
正弦波和餘弦波的三角表示非常直觀,但在數學和工程應用中,使用複數表示波形會更為簡潔且強大。
為什麼?
因為複數能將正弦和餘弦的組合統一到一個公式中,並且方便處理疊加、微分和積分等運算。
在了解複數形式之前,我們先快速回顧複數的基本概念。複數由實部和虛部組成,形式為:
z=a+bi
其中:
- a 是實部。
- b 是虛部。
- i 是虛數單位,滿足 i2=−1。
複數也可以用「極坐標形式」表示為:
z=r(cosθ+isinθ)
這裡:
- r=a2+b2 是複數的模,表示複數從原點到點 (a,b) 的距離。
- θ=tan−1(b/a) 是複數的輻角,表示從實軸正方向逆時針旋轉的角度。
- cosθ 和 sinθ 定義了角度 θ 對應的方向。
在直角坐標中,點 (a,b) 可轉換為極坐標 (r,θ)。
將 r 與 θ 代入三角函數表示,即得 z=r(cosθ+isinθ)。
從數學定義來看,指數函數 ex 可以展開為無窮級數:
ex=1+1!x+2!x2+3!x3+⋯
這個級數在 x 為實數時是直觀的,但它也適用於 x 是複數的情況。
例如,當 x=iθ 時,代入公式得:
eiθ=1+1!iθ+2!(iθ)2+3!(iθ)3+⋯
將 (iθ)n 展開,注意到 i2=−1,i3=−i,i4=1 等週期性,則 eiθ 的展開可分為實部和虛部:
實部項為:
1+2!(iθ)2+4!(iθ)4+⋯=1−2!θ2+4!θ4−⋯
這裡恰好就是 cosθ 的展開式,同理類推,虛部項為:
1!(iθ)+3!(iθ)3+5!(iθ)5+⋯=i(θ−3!θ3+5!θ5−⋯)
這裡也恰好就是 sinθ 的展開式。
因此,綜合實部和虛部,就得到了大名鼎鼎的歐拉公式:
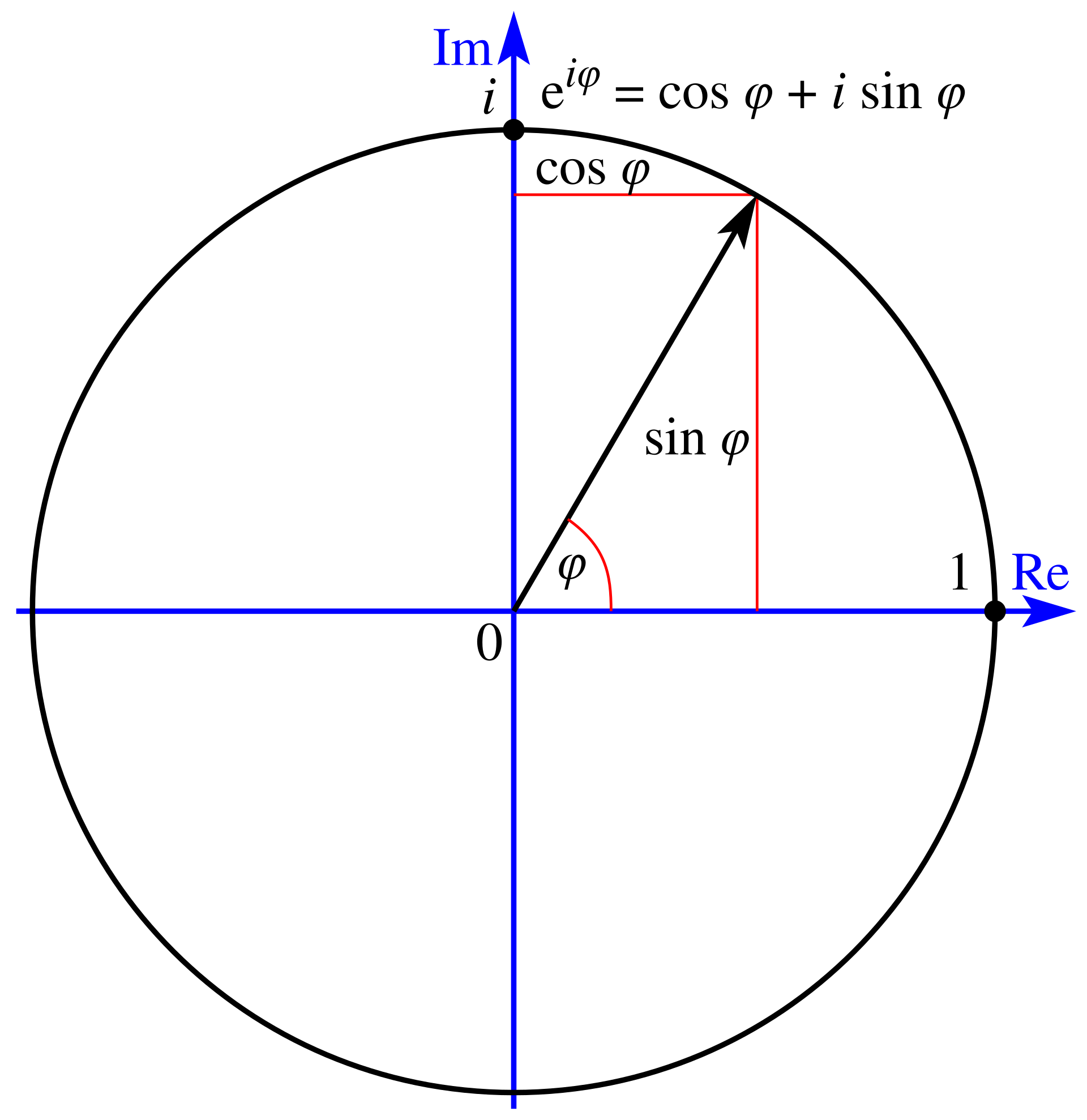
eiθ=cosθ+isinθ
這裡:
- eiθ 是複數的指數表示,包含了實部 cosθ 和虛部 isinθ。
- 複數的實部和虛部分別對應波形的橫向和縱向運動。
這裡可以用歐拉公式來改寫波形公式。例如,考慮以下複數波形:
z(t)=Aei(2πft+ϕ)
將 ei(2πft+ϕ) 展開,利用歐拉公式得到:
z(t)=A[cos(2πft+ϕ)+isin(2πft+ϕ)]
這表示同一個波形同時具有:
- 實部 ℜ(z)=Acos(2πft+ϕ)
- 虛部 ℑ(z)=Asin(2πft+ϕ)
所以,如果想用複數形式表示正弦波與餘弦波,那麼可以用複數的實部和虛部來表示:
-
正弦波 y(t)=Asin(2πft+ϕ):
- 用複數的虛部來表示:
y(t)=ℑ(Aei(2πft+ϕ))
-
餘弦波 y(t)=Acos(2πft+ϕ):
- 用複數的實部來表示:
y(t)=ℜ(Aei(2πft+ϕ))
這裡的 Aei(2πft+ϕ) 是統一的複數表示,實部和虛部分別對應餘弦波和正弦波。
如果用三角函數直接表示兩個波形疊加,需要用到三角函數的加法公式,例如:
cos(A+B)=cosAcosB−sinAsinB
和
sin(A+B)=sinAcosB+cosAsinB
當疊加兩個波形:
y1(t)=A1cos(2πf1t+ϕ1),y2(t)=A2sin(2πf2t+ϕ2)
我們需要分別展開每個波形,處理其中的 cos 和 sin 的加法公式,再整理實部與虛部。
這過程非常繁瑣且容易出錯,特別是當有更多波形參與疊加時,公式的複雜度會呈指數級增長。
除了臺灣的高中生之外,應該沒人會想不開去徒手算這個吧?
在複數形式中,每個波形表示為:
z1=A1ei(2πf1t+ϕ1),z2=A2ei(2πf2t+ϕ2)
疊加波形變成:
z(t)=z1+z2=A1ei(2πf1t+ϕ1)+A2ei(2πf2t+ϕ2)
這裡的關鍵在於,複數的加法是「線性的」,即兩個波形的模長和相位可以直接相加或保持分離,無需展開三角公式來處理。
另一方面,複數自帶實部與虛部,本身已包含了 cos 和 sin 的信息,在複數加法中,實部和虛部分別對應波形的餘弦和正弦分量,因此不需要手動處理三角函數的分解。
複數形式的另一個優點是,它讓我們能夠清晰地將波形的「振幅」和「相位」分離:
- 振幅由模長 ∣z∣ 决定。
- 相位由輻角 arg(z) 决定。
在疊加波形時,這些信息可以單獨處理或一起參與計算,而不需要展開成三角函數的和差公式。例如,若希望簡單地分析疊加後的波形振幅,可以直接計算 ∣z∣=ℜ(z)2+ℑ(z)2。
最後,波形的相位旋轉對應於複數的相角偏移。疊加後的波形如果需要調整相位,只需對 eiθ 添加旋轉角度 Δθ,無需分別調整 cos 和 sin 的相位。
上面說了這麼多,都只是為了可以讓我們可以看懂傅立葉轉換的數學公式。
傅立葉轉換的核心概念是:
這意味著,即使一個信號看起來非常複雜,比如一段音樂、一幅圖像,或者一個脈衝,仍然可以將它拆解成簡單的、基本的波形組合。這些基本波形就是我們熟悉的正弦波和餘弦波,並且它們以不同的頻率、振幅和相位共同組成了信號的全貌。
正弦波和餘弦波具有強大的數學性質。對於任何週期性現象,正弦波和餘弦波可以被視為一組「基底」,就像空間中描述位置的 x,y,z 坐標軸一樣。通過適當的線性組合,能夠表示任何複雜的形狀或變化。
假設一個信號 y(t) 是一個時間變化的函數,傅立葉轉換會幫助我們回答兩個關鍵問題:
- 有哪些頻率存在於這個信號中?
- 每個頻率的振幅和相位是多少?
這種頻率的分解讓我們能夠從完全不同的角度理解信號。相比於直接觀察隨時間變化的波形,可以更清晰地看到信號的頻譜特徵。
傅立葉轉換的數學定義給出了將信號從「時間域」轉換到「頻率域」的方法,核心公式為:
Y(f)=∫−∞∞y(t)e−i2πftdt
其公式各個部分的物理意義如下:
-
原始信號 y(t):
y(t) 是一個定義在時間域上的函數。這可以是任何形式的信號,例如一段音樂的音波、電信號的振幅變化,或者一個在某段時間內跳變的脈衝序列。
y(t) 中包含了信號在每一時刻 t 上的振幅值。
-
複數指數函數 e−i2πft:
這是傅立葉轉換的關鍵部分,實際上它是正弦波和餘弦波的組合:
e−i2πft=cos(2πft)−isin(2πft)
在傅立葉轉換中,e−i2πft 的作用是用一個具有頻率 f 的複數波形去與 y(t) 匹配,提取出信號在該頻率上的強度。
積分操作本質上是一種內積運算,用於衡量 y(t) 與 e−i2πft 的相似程度。
這種「相似度」決定了信號在頻率 f 上的貢獻大小。
傅立葉轉換會對所有可能的頻率 f 進行掃描。
對於每一個 f,通過積分計算得出的值 Y(f) 就是該頻率上的強度,這也是為什麼 Y(f) 稱為「頻譜」的原因。
講這麼多,不如自己動手算算看:
考慮一個單一頻率的信號:
y(t)=Acos(2πf0t+ϕ)
利用歐拉公式,將其表示為:
y(t)=ℜ{Aei(2πf0t+ϕ)}
當我們對其進行傅立葉轉換:
Y(f)=∫−∞∞y(t)e−i2πftdt
將 y(t) 的表示代入,得:
Y(f)=∫−∞∞ℜ{Aei(2πf0t+ϕ)}e−i2πftdt
因為傅立葉轉換的核心是積分操作,它的效果是將時間域上的所有點與一個頻率波形進行匹配。如果 f=f0,則 e−i2πft 和 ei2πf0t 會完全對齊,積分的結果為非零值。
若 f=f0,這兩個波形在相位上不匹配,積分的結果接近零。
當頻率匹配時,可以得到:
Y(f0)=Aeiϕ
這表明頻譜 Y(f) 不僅包含該頻率的強度(由 A 給出),還包含該頻率的相位(由 ϕ 給出)。
這是傅立葉轉換能夠完整描述信號的重要原因。
傅立葉級數是傅立葉轉換的一種特例,它主要用於處理週期性信號。
與傅立葉轉換可以將信號的頻譜延伸到連續的頻率範圍不同,傅立葉級數專注於用一組「離散頻率」來描述週期性信號。
傅立葉級數的核心概念是:
- 任何週期性信號都可以表示為一組「離散頻率」的正弦波和餘弦波的線性組合。
這表示,只要信號是週期性的,我們就可以用有限數目的正弦波和餘弦波來逼近該信號,且隨著頻率組合的增加,逼近的精度會越高。
假設一個週期為 T 的信號 x(t),可以用傅立葉級數表示為:
x(t)=a0+n=1∑∞[ancos(T2πnt)+bnsin(T2πnt)]
其中,a0,an,bn 是傅立葉級數的係數,分別表示不同頻率下的正弦波和餘弦波的振幅,這些係數的具體值由下列公式決定:
-
直流分量(a0):
a0=T1∫0Tx(t)dt
它表示信號的平均值,亦即信號在整個週期內的直流分量。
-
餘弦波係數(an):
an=T2∫0Tx(t)cos(T2πnt)dt
它表示信號中對應於頻率 Tn 的餘弦波的振幅。
-
正弦波係數(bn):
bn=T2∫0Tx(t)sin(T2πnt)dt
它表示信號中對應於頻率 Tn 的正弦波的振幅。
同樣地,為了簡化表示和計算,傅立葉級數通常也會以複數形式表示:
x(t)=n=−∞∑∞cneiT2πnt
其中,cn 是複數係數,定義為:
cn=T1∫0Tx(t)e−iT2πntdt
在這種形式中:
- 實部 ℜ{cn} 與 an 對應。
- 虛部 ℑ{cn} 與 bn 對應。
傅立葉級數在工程和科學中有著廣泛的應用,例如研究機械結構中的周期性振動,分析週期性電信號,例如方波、三角波、鋸齒波等。
在這裡只能簡短介紹一下傅立葉轉換的相關內容。
後續還有離散傅立葉變換(DFT)與快速傅立葉變換(FFT)、傅立葉變換與卷積的關係、頻域濾波的設計與實現以及傅立葉分析在量子物理與影像處理中的延伸等等,講個三天三夜也講不完。
有興趣的讀者可以自行查閱相關資料,進一步了解傅立葉轉換的原理和應用。
剩下一點篇幅,我寫個遊樂設施放在最後,一起來感受一下傅立葉的魅力吧!
根據設定,程式會在時域上繪製對應的波形,並觀察其在頻域上的分析結果。
你會看到頻域上的分佈結果和「設定面板」上的數值一致,其餘的頻率是為了要近似這個波形而產生的。