[19.11] MQA

共有キーと値

Fast Transformer Decoding: One Write-Head is All You Need

共有経済が盛況であり、注意機構にも同様のアプローチを適用できるようです。

この論文の著者は Noam Shazeer であり、「Attention is all you need」の著者グループの一員です。

問題の定義

著者は一般的な注意機構を提案した後、デコードの過程で自回帰的に出力するため、各位置で全てのキーとバリューを計算する必要があり、これが大量の重複計算を引き起こすことに気付きました。

この操作は非常に非効率的であり、著者はこれを改善する余地があると考えました。

注意機構の復習

著者がどのようにこの問題を改善したかを知るためには、元々の注意機構から見ていく必要があります。

ヒント

この過程では大量の einsum 演算子が使用され、行列計算を表現しています。もしこの演算子に不慣れであれば、以下の関連する記事を参照してください：

Einsum is All you Need

この論文では tf.einsum が使用されていますが、PyTorch を使っている場合は torch.einsum に変更できます。

今、あなたが einsum 演算子の使い方を熟知していると仮定しています。

警告

数学的警告： 以下の段落では大量の行列演算が行われます。これらの詳細が必要ない場合は、結論の部分に直接進んでください。

結論

Dot-Product Att

まず、単一のクエリベクトル（query）と一連のキー・バリュー対（keys-values）の関係を処理する方法を紹介します。

def DotProductAttention(q, K, V):
    """
    単一のクエリに対するドット積注意機構。
    引数:
    q: 形状が [k] のベクトル（クエリベクトル）
    K: 形状が [m, k] の行列（キーの集合）
    V: 形状が [m, v] の行列（バリューの集合）

    戻り値:
    y: 形状が [v] のベクトル（出力ベクトル）
    """
    # クエリベクトル q とキー行列 K のドット積を計算し、logits（形状は [m]）を生成
    logits = tf.einsum("k,mk->m", q, K)

    # logits に softmax を適用し、各キーの重み（形状は [m]）を計算
    weights = tf.nn.softmax(logits)

    # 重みを使用してバリュー行列 V を加重平均し、出力ベクトル y（形状は [v]）を生成
    y = tf.einsum("m,mv->v", weights, V)

    return y

これは、クラシックなドット積注意機構です。

クエリとキーをドット積で比較し、類似度に基づいてバリューを加重平均し、最終的に出力ベクトルを生成します。

Multi-head Att

次に、マルチヘッド注意機構を紹介します。これは、複数のドット積注意機構を組み合わせることで、モデルの性能を向上させる手法です。

以下の関数では、パラメータの意味は次の通りです：

$d$ ：クエリベクトルの次元
$m$ ：キー・バリュー対の数
$h$ ：注意機構のヘッド数
$k$ ：クエリとキーの線形射影の次元
$v$ ：バリューの線形射影の次元

import tensorflow as tf

def MultiheadAttention(x, M, P_q, P_k, P_v, P_o):
    """
    単一のクエリに対するマルチヘッド注意機構。

    引数:
    x: 形状が [d] のベクトル（クエリベクトル）
    M: 形状が [m, d] の行列（キーとバリューの行列）
    P_q: 形状が [h, d, k] のテンソル（クエリの線形射影行列）
    P_k: 形状が [h, d, k] のテンソル（キーの線形射影行列）
    P_v: 形状が [h, d, v] のテンソル（バリューの線形射影行列）
    P_o: 形状が [h, d, v] のテンソル（出力の線形射影行列）

    戻り値:
    y: 形状が [d] のベクトル（最終的な出力ベクトル）
    """

    # クエリベクトル x の線形射影（形状は [h, k]）
    q = tf.einsum("d, hdk->hk", x, P_q)

    # キーとバリュー行列 M の線形射影
    # キー行列 K の形状は [h, m, k]、バリュー行列 V の形状は [h, m, v]
    K = tf.einsum("md, hdk->hmk", M, P_k)
    V = tf.einsum("md, hdv->hmv", M, P_v)

    # クエリとキーのドット積（logits）を計算（形状は [h, m]）
    logits = tf.einsum("hk, hmk->hm", q, K)

    # softmax を使用して注意機構の重みを計算（形状は [h, m]）
    weights = tf.nn.softmax(logits)

    # 重みを使用してバリュー行列を加重平均（形状は [h, v]）
    o = tf.einsum("hm, hmv->hv", weights, V)

    # マルチヘッドの出力を線形射影し、最終的な出力ベクトル（形状は [d]）を生成
    y = tf.einsum("hv, hdv->d", o, P_o)

    return y

Multi-head Att (Batched)

次に、バッチ入力に対応するように拡張します。

一般的な訓練では、バッチ処理を使用するため、上記の関数を変更する必要があります。

import tensorflow as tf

def MultiheadAttentionBatched(X, M, mask, P_q, P_k, P_v, P_o):
    """
    バッチ入力に対するマルチヘッド注意機構。

    引数:
    X: 形状が [b, n, d] のテンソル（クエリベクトル、バッチサイズ b、シーケンス長 n、ベクトル次元 d）
    M: 形状が [b, m, d] のテンソル（キーとバリュー行列、m はキーとバリューの数）
    mask: 形状が [b, h, n, m] のテンソル、不正な注意位置をマスクするために使用
    P_q: 形状が [h, d, k] のテンソル（クエリの線形射影行列）
    P_k: 形状が [h, d, k] のテンソル（キーの線形射影行列）
    P_v: 形状が [h, d, v] のテンソル（バリューの線形射影行列）
    P_o: 形状が [h, d, v] のテンソル（出力の線形射影行列）

    戻り値:
    Y: 形状が [b, n, d] のテンソル（最終的な出力結果）
    """

    # クエリベクトル X の線形射影（形状は [b, h, n, k]）
    Q = tf.einsum("bnd, hdk->bhnk", X, P_q)

    # キーとバリュー行列 M の線形射影、キー K の形状は [b, h, m, k]、バリュー V の形状は [b, h, m, v]
    K = tf.einsum("bmd, hdk->bhmk", M, P_k)
    V = tf.einsum("bmd, hdv->bhmv", M, P_v)

    # クエリとキーのドット積（logits）を計算（形状は [b, h, n, m]）
    logits = tf.einsum("bhnk, bhmk->bhnm", Q, K)

    # mask を logits に適用し、softmax を使用して注意機構の重みを計算（形状は [b, h, n, m]）
    weights = tf.nn.softmax(logits + mask)

    # 重みを使用してバリュー行列を加重平均（形状は [b, h, n, v]）
    O = tf.einsum("bhnm, bhmv->bhnv", weights, V)

    # マルチヘッドの出力を線形射影し、最終的な出力ベクトル（形状は [b, n, d]）を生成
    Y = tf.einsum("bhnv, hdv->bnd", O, P_o)

    return Y

ここでは、計算とメモリアクセスに関する簡略化された仮定がなされています：

$m = n$ ：キーとバリューの数 $m$ がクエリのシーケンス長 $n$ と等しいと仮定します。
$k = v = \frac{d}{h}$ ：Transformer の元の論文に基づき、クエリとキーの次元 $k$ はバリューの次元 $v$ と等しく、またそれらは特徴次元 $d$ と比例し、その比例係数はヘッドの数 $h$ です。
$n ≤ d$ ：シーケンス長 $n$ は特徴次元 $d$ より小さいか等しいと仮定します。

これらの仮定に基づいて、計算の総量は $Θ(bnd^2)$ です。ここで、 $b$ はバッチサイズ、 $n$ はシーケンス長、 $d$ は特徴次元です。これは、各 tf.einsum 操作の複雑度が $O(bnd^2)$ であるためです。

ヒント

例えば、1000 個のシーケンスがあり、各シーケンスの長さが 100、ベクトルの次元が 512 の場合、計算量はおおよそ $1000 \times 100 \times 512^2$ になります。

メモリアクセスのサイズに関して、すべてのテンソルの総メモリ需要は $O(bnd + bhn^2 + d^2)$ です：

第一項 $bnd$ は入力 $X$ 、キーとバリュー行列 $M$ 、クエリ $Q$ 、キー $K$ 、バリュー $V$ 、出力 $O$ 、最終的な出力 $Y$ から来ています。
第二項 $bhn^2$ は logits と重みから来ています。
第三項 $d^2$ は投影テンソル $P_q$ 、 $P_k$ 、 $P_v$ 、 $P_o$ から来ています。

メモリアクセスと計算の比率は次のようになります：

O\left(\frac{1}{k} + \frac{1}{bn}\right)

この比率が低いほど、現代の GPU/TPU ハードウェアの性能に有利です。なぜなら、これらのハードウェアの計算能力はメモリ帯域幅を大きく上回るためです。

Multi-head Att (Incremental)

一般的なマルチヘッド注意機構に加えて、自己回帰に基づくインクリメンタルな注意機構があります。

import tensorflow as tf

def MultiheadSelfAttentionIncremental(x, prev_K, prev_V, P_q, P_k, P_v, P_o):
    """
    インクリメンタル生成の1ステップにおけるマルチヘッド自己注意機構。

    引数:
    x: 形状が [b, d] のテンソル、現在のステップのクエリベクトル
    prev_K: 形状が [b, h, m, k] のテンソル、前のステップのキー行列
    prev_V: 形状が [b, h, m, v] のテンソル、前のステップのバリュー行列
    P_q: 形状が [h, d, k] のテンソル、クエリベクトルの線形射影行列
    P_k: 形状が [h, d, k] のテンソル、キーの線形射影行列
    P_v: 形状が [h, d, v] のテンソル、バリューの線形射影行列
    P_o: 形状が [h, d, v] のテンソル、出力の線形射影行列

    戻り値:
    y: 形状が [b, d] のテンソル、現在のステップの出力結果
    new_K: 形状が [b, h, m+1, k] のテンソル、更新後のキー行列
    new_V: 形状が [b, h, m+1, v] のテンソル、更新後のバリュー行列
    """

    # クエリベクトル x の線形射影を計算（形状は [b, h, k]）
    q = tf.einsum("bd, hdk->bhk", x, P_q)

    # キー行列を更新し、現在のステップの新しいキーを前のキー行列に連結（形状は [b, h, m+1, k]）
    new_K = tf.concat(
        [prev_K, tf.expand_dims(tf.einsum("bd, hdk->bhk", x, P_k), axis=2)],
        axis=2
    )

    # バリュー行列を更新し、現在のステップの新しいバリューを前のバリュー行列に連結（形状は [b, h, m+1, v]）
    new_V = tf.concat(
        [prev_V, tf.expand_dims(tf.einsum("bd, hdv->bhv", x, P_v), axis=2)],
        axis=2
    )

    # クエリとキーのドット積（logits）を計算（形状は [b, h, m]）
    logits = tf.einsum("bhk, bhmk->bhm", q, new_K)

    # softmax を使って注意重みを計算（形状は [b, h, m]）
    weights = tf.nn.softmax(logits)

    # 重みを使ってバリュー行列を加重平均（形状は [b, h, v]）
    o = tf.einsum("bhm, bhmv->bhv", weights, new_V)

    # マルチヘッド出力を線形射影し、最終的な出力ベクトル（形状は [b, d]）を生成
    y = tf.einsum("bhv, hdv->bd", o, P_o)

    return y, new_K, new_V

著者は以前の簡略化された仮定を引き継ぎ、インクリメンタル推論の性能評価を行っています。

推論の全体的な計算量は $\Theta(bnd^2)$ であり、ここで $b$ はバッチサイズ、 $n$ はシーケンス長、 $d$ は特徴次元です。

メモリアクセスの合計量は $\Theta(bn^2d + nd^2)$ です：

第一項 $bn^2d$ は、各ステップでキー $K$ とバリュー $V$ を再ロードするメモリ操作から来ており、これらのテンソルのサイズはシーケンス長 $n$ に比例して増加します。
第二項 $nd^2$ は、クエリ、キー、バリューの線形射影行列 $P_q, P_k, P_v, P_o$ から来ています。

メモリアクセスと計算の比率は次のように示されます：

\Theta\left(\frac{n}{d} + \frac{1}{b}\right)

もし $n ≈ d$ または $b ≈ 1$ であれば、この比率は 1 に近づき、メモリ帯域幅が現代の計算ハードウェアにおける主要なボトルネックとなることを意味します。

比較的簡単な最適化戦略は、バッチサイズを増加させることで、メモリアクセスと計算の比率を容易に減少させることができます。

もう一つの方法は $\frac{n}{d}$ の比率を減少させる ことですが、これは各ステップでキーとバリューのテンソルを再ロードする必要があるため、難易度が高いです。最適化手法には、シーケンス長 $n$ を制限することや、ローカルな範囲内でのみ注意機構を計算して、処理するメモリ位置の数を圧縮する方法が含まれます。

解決問題

鍵和值テンソルのサイズを減らすために、著者が提案した具体的な方法は、 $\text{Key}$ と $\text{Value}$ の「ヘッド」（heads）次元を取り除き、クエリにおける「ヘッド」次元を保持することで、メモリ負担を減らし、効率を向上させることです。

Multi-Query Attention

多クエリ注意機構（Multi-Query Attention）は、多頭注意機構（Multi-Head Attention）の一種の変種です。

従来の多頭注意機構では、異なる「ヘッド」が独立したクエリ（queries）、キー（keys）、バリュー（values）、および出力を持っていますが、多クエリ注意機構ではこの構造が簡略化されています：異なるヘッドは一組のキーとバリューを共有し、クエリの多頭構造のみを保持します。これにより、メモリの負担が軽減され、推論速度が向上します。

def MultiQueryAttentionBatched(X, M, mask, P_q, P_k, P_v, P_o):
    """
    バッチ入力に対する多クエリ注意機構。

    引数:
    X: 形状が [b, n, d] のテンソル、クエリベクトル
    M: 形状が [b, m, d] のテンソル、キーとバリューの行列
    mask: 形状が [b, h, n, m] のテンソル、不正な位置をマスクするために使用
    P_q: 形状が [h, d, k] のテンソル、クエリベクトルの線形射影
    P_k: 形状が [d, k] のテンソル、キーの線形射影
    P_v: 形状が [d, v] のテンソル、バリューの線形射影
    P_o: 形状が [h, d, v] のテンソル、出力ベクトルの線形射影

    戻り値:
    Y: 形状が [b, n, d] のテンソル、最終的な出力結果
    """

    # クエリベクトル X の線形射影（形状は [b, h, n, k]）
    Q = tf.einsum("bnd, hdk->bhnk", X, P_q)

    # キーとバリュー行列 M の線形射影、キー K は [b, m, k]、バリュー V は [b, m, v]
    K = tf.einsum("bmd, dk->bmk", M, P_k)
    V = tf.einsum("bmd, dv->bmv", M, P_v)

    # クエリとキーのドット積を計算（形状は [b, h, n, m]）
    logits = tf.einsum("bhnk, bmk->bhnm", Q, K)

    # softmax を適用して注意重みを計算し、マスクを考慮
    weights = tf.nn.softmax(logits + mask)

    # 重みを使ってバリューを加重平均（形状は [b, h, n, v]）
    O = tf.einsum("bhnm, bmv->bhnv", weights, V)

    # 最終的な線形射影と統合（形状は [b, n, d]）
    Y = tf.einsum("bhnv, hdv->bnd", O, P_o)

    return Y

著者は増分多クエリ自己注意機構（Incremental Multi-Query Self-Attention）の実装コードも提供しています：

def MultiQuerySelfAttentionIncremental(x, prev_K, prev_V, P_q, P_k, P_v, P_o):
    """
    1ステップの増分多クエリ自己注意機構。

    引数:
    x: 形状が [b, d] のテンソル、現在のステップのクエリベクトル
    prev_K: 形状が [b, m, k] のテンソル、前のステップのキー行列
    prev_V: 形状が [b, m, v] のテンソル、前のステップのバリュー行列
    P_q: 形状が [h, d, k] のテンソル、クエリの線形射影
    P_k: 形状が [d, k] のテンソル、キーの線形射影
    P_v: 形状が [d, v] のテンソル、バリューの線形射影
    P_o: 形状が [h, d, v] のテンソル、出力の線形射影

    戻り値:
    y: 形状が [b, d] のテンソル、出力結果
    new_K: 更新されたキー行列、形状は [b, m+1, k]
    new_V: 更新されたバリュー行列、形状は [b, m+1, v]
    """

    # クエリベクトルの線形射影（形状は [b, h, k]）
    q = tf.einsum("bd, hdk->bhk", x, P_q)

    # キーとバリュー行列を更新
    new_K = tf.concat([prev_K, tf.expand_dims(tf.einsum("bd, dk->bk", x, P_k), axis=2)], axis=2)
    new_V = tf.concat([prev_V, tf.expand_dims(tf.einsum("bd, dv->bv", x, P_v), axis=2)], axis=2)

    # クエリとキーのドット積（形状は [b, h, m]）を計算
    logits = tf.einsum("bhk, bmk->bhm", q, new_K)

    # softmax を使って重みを計算
    weights = tf.nn.softmax(logits)

    # 重みを使ってバリューを加重平均
    o = tf.einsum("bhm, bmv->bhv", weights, new_V)

    # 線形射影して出力を統合
    y = tf.einsum("bhv, hdv->bd", o, P_o)

    return y, new_K, new_V

性能分析

従来の多頭注意機構と同様に、インクリメンタル多クエリ注意機構では、計算量は依然として $\Theta(bnd^2)$ であり、メモリアクセス量は $\Theta(bnd + bn^2k + nd^2)$ です。

キーとバリューの「ヘッド」次元を削減することにより、メモリの消費は大幅に減少し、計算効率は顕著に向上します。

ヒント

仮定として、ヘッド数 $h = 8$ 、キーの次元 $k = \frac{d}{h} = \frac{512}{8} = 64$ とすると、これは従来の多頭注意機構の要求よりも低くなります。なぜなら、従来の多頭注意機構のアクセス量は $\Theta(bnd + bhn^2 + d^2)$ であり、ここにヘッド数 $h$ に依存する項が追加されているからです。

メモリアクセスと計算の比率は次のように表されます：

\Theta\left(\frac{1}{d} + \frac{n}{dh} + \frac{1}{b}\right)

ここで、 $\frac{n}{d}$ の項がヘッド数 $h$ によって削減され、これによりインクリメンタル推論の性能が大幅に向上します。

ヒント

従来の多頭注意機構の比率： $\Theta\left(\frac{n}{d} + \frac{1}{b}\right)$

従来の多頭注意機構では、メモリアクセスと計算の比率はシーケンス長 $n$ と特徴次元 $d$ の比率に影響されます。シーケンス長が特徴次元に近い場合、この比率は 1 に近づき、メモリアクセスが性能のボトルネックとなります。
多クエリ注意機構の比率： $\Theta\left(\frac{1}{d} + \frac{n}{dh} + \frac{1}{b}\right)$

キーとバリューの次元が削減され、ここでの $n/d$ の比率は $h$ によって $h$ 倍減少します。仮に $h = 8$ とすると、メモリアクセス量が大幅に減少し、推論効率が大きく向上します。

例えば、言語モデルの生成を行っていると仮定し、バッチサイズ $b = 128$ 、シーケンス長 $n = 100$ の単語を処理する場合（各単語のベクトル次元 $d = 512$ ）、

従来の多頭注意機構での「メモリアクセス-計算比」は次のように計算されます：

\frac{n}{d} + \frac{1}{b} = \frac{100}{512} + \frac{1}{128} \approx 0.195 + 0.0078 = 0.2028

一方、 $h = 8$ の多クエリ注意機構では、この比率は次のようになります：

\frac{1}{d} + \frac{n}{dh} + \frac{1}{b}

= \frac{1}{512} + \frac{100}{512 \times 8} + \frac{1}{128}

\approx 0.00195 + 0.0244 + 0.0078 = 0.03415

簡単に計算してみると、多クエリ注意機構がメモリアクセスと計算量の比率を効果的に低減させ、これが全体的な推論効率の向上に繋がることがわかります。

訓練策略

著者は WMT 2014 英独翻訳タスクを使用して評価を行いました。

モデルは 6 層のエンコーダ・デコーダ Transformer モデルを使用し、以下の設定を採用しています：

$d_{model} = 1024$
$d_{ff} = 4096$
ヘッド数 $h = 8$
$d_k = d_v = 128$ 、学習可能な位置エンベディングを使用し、トークンエンベディング層と出力層の間で重みを共有

訓練は 20 エポック行い、各バッチには 128 サンプルが含まれ、各サンプルには 256 トークンの入力シーケンスと 256 トークンのターゲットシーケンスがあります。モデルは 32 コアの TPUv3 クラスター上で訓練され、各モデルの訓練時間は約 2 時間です。

MQA モデルでは、著者はモデル内のすべての注意機構層を Multi-Query 注意機構に置き換え、フィードフォワード層の隠れ層の次元を 4096 から 5440 に増加させ、総パラメータ数をベースラインモデルと一致させています。

討論

WMT14 EN-DE 結果

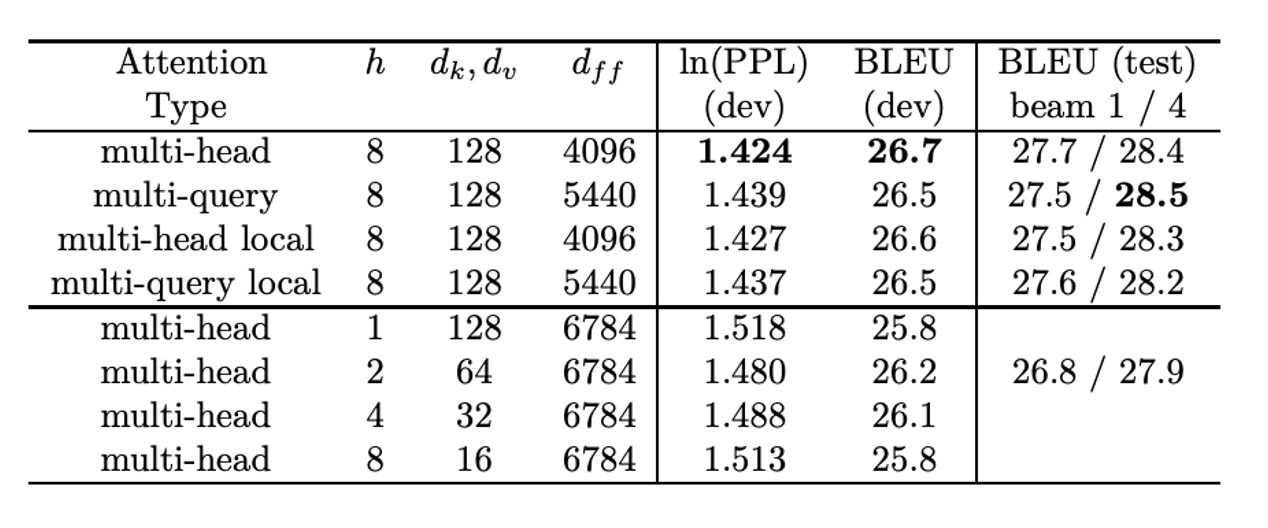
WMT14 EN-DE

上表は著者提供の実験データです。

表から、Multi-Query 注意機構モデルはベースラインモデルに「若干劣る」ことがわかりますが、 $h$ 、 $d_k$ 、 $d_v$ を削減した他の変種よりも優れた性能を示しています。

推論時間の改善

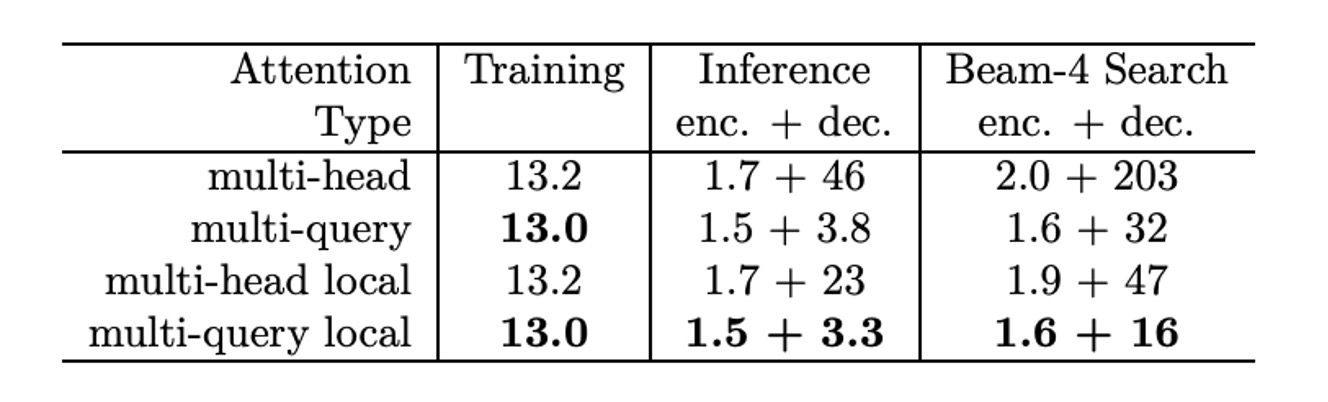
Inference Time

訓練速度については、TPUv2（8 コア） を使用した訓練速度テストで、各訓練ステップで 32,768 トークンを処理した結果です。

ベースラインモデル：各ステップの訓練時間は 433ms。
多クエリモデル：各ステップの訓練時間は 425ms、ベースラインモデルよりやや速い。

各トークンの訓練時間は次の通りです：

ベースラインモデル：
$\frac{433}{32,768} = 13.2\mu s$
MQA モデル：
$\frac{425}{32,768} = 13.0\mu s$

次に、自己回帰モデルを使用して、1024 のシーケンス（各シーケンスに 128 トークン、平均して各 TPU コアで 128 シーケンスを処理）の場合における増分貪欲デコードの推論速度をテストしました。

ベースラインモデル：
- エンコーダ部分の時間は 222ms で、各トークンの時間は 1.7µs です。
- デコーダは各ステップで 47ms かかり、各トークンのデコード時間は 46µs です。
MQA モデル：
- エンコーダ部分の時間は 195ms で、各トークンの時間は 1.5µs です。
- デコーダは各ステップで 3.9ms かかり、各トークンのデコード時間は 3.8µs で、ベースラインモデルより大幅に速いです。

結論

速くて効率的！

精度にほとんど損失を与えることなく、推論速度を大幅に向上させ、特に自己回帰モデルでは約 10 倍の向上を実現しました！

ヒント

このアーキテクチャは、後続の MobileNet V4 でも再び使用されています。興味がある読者は以下を確認できます：

[24.04] MobileNet-V4: 五年後の継承

共有キーと値​

問題の定義​

注意機構の復習​

Dot-Product Att​

Multi-head Att​

Multi-head Att (Batched)​

Multi-head Att (Incremental)​

解決問題​

Multi-Query Attention​

性能分析​

訓練策略​

討論​

WMT14 EN-DE 結果​

推論時間の改善​

結論​