[20.10] Deformable DETR

Z. Yuan

Dosaid maintainer, Full-Stack AI Engineer

可變形的注意力機制

Deformable DETR: Deformable Transformers for End-to-End Object Detection

DETR 留給研究者們一個很好發揮的空間。

它只用了最基本的 Transformer 架構，做最樸素的物件偵測。裡面也沒有用到什麼提升分數的技巧，只是單純的把圖片丟進去，然後就可以得到物件的位置和類別。

多麽美好的論文！

往後的研究者們只要基於這個思路改進模型，論文還不是刷刷刷一大把？

定義問題

和目前的物件偵測器相比，DETR 實在是太慢了。

如果我們把它和時下最流行的 Faster-RCNN 比起來，推論速度慢了 2 倍！

那又怎樣？感覺好像也不是什麼大問題？

沒錯，問題不在推論速度，而是訓練收斂速度，慢了 20 倍！

原本只需要 1 天的訓練時間，現在變成需要 20 天，這是多麽可怕的事情？

韶光易逝，年華易老。等模型收斂，等到頭髮都白了。

這不行，肯定要改。

解決問題

作者認為問題出在 Transformer 的注意力機制上。

在圖片上使用 Transformer，每個 pixel 都要對其他所有 pixel 做注意力運算，這表示大部分的算力都浪費在無效的地方。

所以這裡不能再使用原本的 Transformer 注意力機制，而是借鑒了「可變形卷積」的思路，將原本的注意力機制改成一種「可變形的注意力機制」。

提示

此時 ViT 尚未發表，因此操作的時候都是基於每個像素點，而不是每個切分影像區塊。

可變形注意力

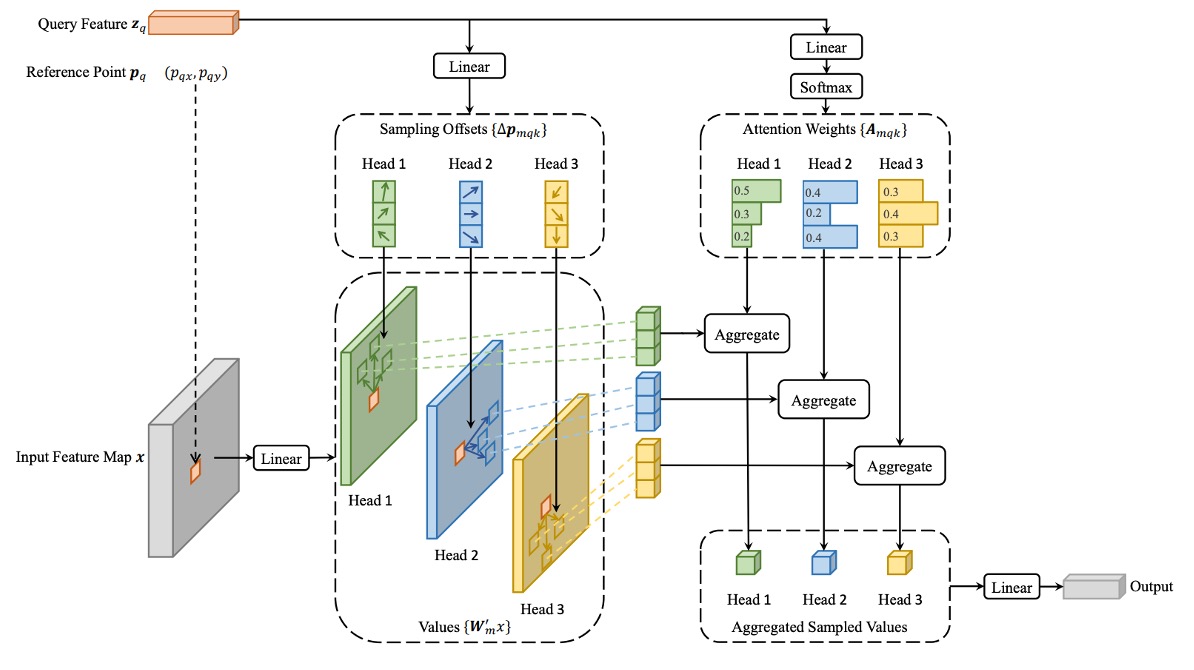
deformable attention

在圖像特徵圖中，給定每個查詢元素（Query Element），有別於傳統 Transformer，作者會選擇一個參考點作為基準，並且在其周圍的一些重要採樣點進行注意力操作。

假設輸入的特徵圖為：

x \in \mathbb{R}^{C \times H \times W}

其中 $C$ 表示通道數， $H$ 和 $W$ 分別是特徵圖的高度和寬度。

查詢元素 $q$ 包含一個內容特徵 $z_q$ 和一個 2D 參考點 $p_q$ ，可變形注意力特徵的計算公式如下：

\text{DeformAttn}(z_q, p_q, x) = \sum_{m=1}^{M} W_m \sum_{k=1}^{K} A_{mqk} \cdot W_m^{\prime} x(p_q + \Delta p_{mqk})

其中：

$M$ 表示注意力頭的數量。
$K$ 表示每個查詢點所選擇的採樣點數量，這些點從參考點附近的一小區域中選取。
$A_{mqk}$ 是第 $m$ 個注意力頭中第 $k$ 個採樣點的注意力權重，範圍在 $[0, 1]$ 之間。
$\Delta p_{mqk}$ 是第 $m$ 個注意力頭中第 $k$ 個採樣點的偏移量，這些偏移量可以是任意的實數。
$W_m$ 和 $W_m^{\prime}$ 是可學習的權重矩陣，負責將輸入特徵進行線性變換。
$x(p_q + \Delta p_{mqk})$ 表示在位置 $p_q + \Delta p_{mqk}$ 處的特徵值，因為該位置是分數值（即非整數點），因此使用雙線性插值來計算。

查詢特徵 $z_q$ 經過一個線性投影操作，該操作會輸出一個 $3mk$ 通道的張量：

前 $2mk$ 個通道用來編碼每個採樣點的偏移量 $\Delta p_{mqk}$ 。
剩餘的 $mk$ 個通道會經過 softmax 操作，計算出對應的注意力權重 $A_{mqk}$ 。

這種設計方式，可以保證「偏移量」與「注意力權重」都是從查詢元素的特徵中學習得到的，而不是基於固定的規則。

多尺度計算

現代物件偵測框架通常會使用多尺度特徵圖來進行物件偵測。

可變形注意力模組當然也得支援多尺度版本，允許同時在多個特徵圖層上進行採樣和操作。

假設輸入的多尺度特徵圖為 $\{x_l\}_{l=1}^L$ ，每個特徵圖 $x_l \in \mathbb{R}^{C \times H_l \times W_l}$ 。

查詢元素的參考點用正規化坐標 $\hat{p}_q \in [0, 1]^2$ 表示，則多尺度的計算公式為：

\text{MSDeformAttn}(z_q, \hat{p}_q, \{x_l\}_{l=1}^L) =

\sum_{m=1}^{M} W_m \sum_{l=1}^{L} \sum_{k=1}^{K} A_{mlqk} \cdot W_m^{\prime} x_l(\phi_l(\hat{p}_q) + \Delta p_{mlqk})

$L$ 表示輸入的特徵圖層數量。
$\phi_l(\hat{p}_q)$ 是一個縮放函數，用來將正規化坐標轉換到第 $l$ 層特徵圖上的實際坐標。
其他符號的意義與單尺度的情況類似。

模型架構

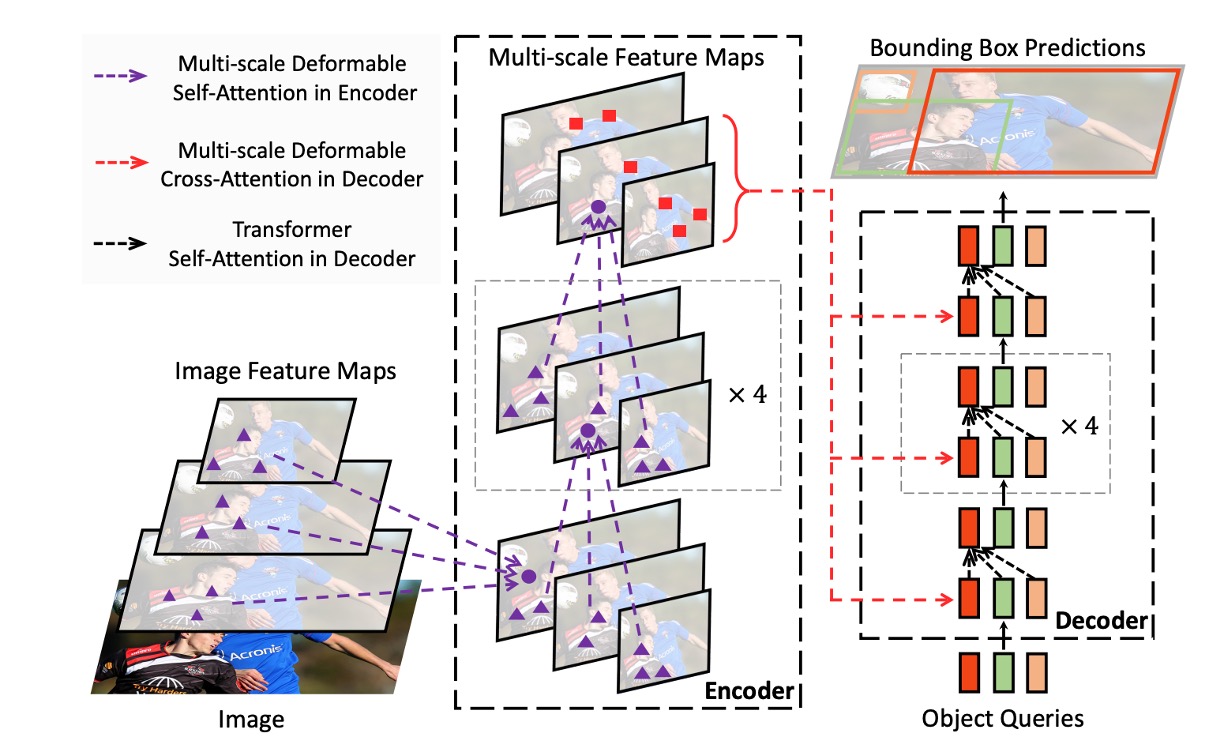
model

如上圖，當我們解決了可變形注意力的問題之後，把原本 DETR 架構中的 Transformer 模組全部抽換掉，於是就得到了 Deformable DETR。

資訊

如果理論知識你不感興趣，也可以直接到官方的 Github 上取得他們的實作。

fundamentalvision/Deformable-DETR

程式碼拆解

我們單獨把作者的實作拿出來看一下，到底 MSDeformAttn 和一般的 Attn 有什麼差異：

class MSDeformAttn(nn.Module):

    def __init__(self, d_model=256, n_levels=4, n_heads=8, n_points=4):
        """
        Multi-Scale Deformable Attention Module
        :param d_model      hidden dimension
        :param n_levels     number of feature levels
        :param n_heads      number of attention heads
        :param n_points     number of sampling points per attention head per feature level
        """
        super().__init__()
        if d_model % n_heads != 0:
            raise ValueError('d_model must be divisible by n_heads, but got {} and {}'.format(d_model, n_heads))
        _d_per_head = d_model // n_heads
        # you'd better set _d_per_head to a power of 2 which is more efficient in our CUDA implementation
        if not _is_power_of_2(_d_per_head):
            warnings.warn("You'd better set d_model in MSDeformAttn to make the dimension of each attention head a power of 2 "
                          "which is more efficient in our CUDA implementation.")

        self.im2col_step = 64

        self.d_model = d_model
        self.n_levels = n_levels
        self.n_heads = n_heads
        self.n_points = n_points

        self.sampling_offsets = nn.Linear(d_model, n_heads * n_levels * n_points * 2)
        self.attention_weights = nn.Linear(d_model, n_heads * n_levels * n_points)
        self.value_proj = nn.Linear(d_model, d_model)
        self.output_proj = nn.Linear(d_model, d_model)

        self._reset_parameters()

    def _reset_parameters(self):
        constant_(self.sampling_offsets.weight.data, 0.)
        thetas = torch.arange(self.n_heads, dtype=torch.float32) * (2.0 * math.pi / self.n_heads)
        grid_init = torch.stack([thetas.cos(), thetas.sin()], -1)
        grid_init = (grid_init / grid_init.abs().max(-1, keepdim=True)[0]).view(self.n_heads, 1, 1, 2).repeat(1, self.n_levels, self.n_points, 1)
        for i in range(self.n_points):
            grid_init[:, :, i, :] *= i + 1
        with torch.no_grad():
            self.sampling_offsets.bias = nn.Parameter(grid_init.view(-1))
        constant_(self.attention_weights.weight.data, 0.)
        constant_(self.attention_weights.bias.data, 0.)
        xavier_uniform_(self.value_proj.weight.data)
        constant_(self.value_proj.bias.data, 0.)
        xavier_uniform_(self.output_proj.weight.data)
        constant_(self.output_proj.bias.data, 0.)

    def forward(self, query, reference_points, input_flatten, input_spatial_shapes, input_level_start_index, input_padding_mask=None):
        """
        :param query                       (N, Length_{query}, C)
        :param reference_points            (N, Length_{query}, n_levels, 2), range in [0, 1], top-left (0,0), bottom-right (1, 1), including padding area
                                        or (N, Length_{query}, n_levels, 4), add additional (w, h) to form reference boxes
        :param input_flatten               (N, \sum_{l=0}^{L-1} H_l \cdot W_l, C)
        :param input_spatial_shapes        (n_levels, 2), [(H_0, W_0), (H_1, W_1), ..., (H_{L-1}, W_{L-1})]
        :param input_level_start_index     (n_levels, ), [0, H_0*W_0, H_0*W_0+H_1*W_1, H_0*W_0+H_1*W_1+H_2*W_2, ..., H_0*W_0+H_1*W_1+...+H_{L-1}*W_{L-1}]
        :param input_padding_mask          (N, \sum_{l=0}^{L-1} H_l \cdot W_l), True for padding elements, False for non-padding elements

        :return output                     (N, Length_{query}, C)
        """
        N, Len_q, _ = query.shape
        N, Len_in, _ = input_flatten.shape
        assert (input_spatial_shapes[:, 0] * input_spatial_shapes[:, 1]).sum() == Len_in

        value = self.value_proj(input_flatten)
        if input_padding_mask is not None:
            value = value.masked_fill(input_padding_mask[..., None], float(0))
        value = value.view(N, Len_in, self.n_heads, self.d_model // self.n_heads)
        sampling_offsets = self.sampling_offsets(query).view(N, Len_q, self.n_heads, self.n_levels, self.n_points, 2)
        attention_weights = self.attention_weights(query).view(N, Len_q, self.n_heads, self.n_levels * self.n_points)
        attention_weights = F.softmax(attention_weights, -1).view(N, Len_q, self.n_heads, self.n_levels, self.n_points)
        # N, Len_q, n_heads, n_levels, n_points, 2
        if reference_points.shape[-1] == 2:
            offset_normalizer = torch.stack([input_spatial_shapes[..., 1], input_spatial_shapes[..., 0]], -1)
            sampling_locations = reference_points[:, :, None, :, None, :] \
                                 + sampling_offsets / offset_normalizer[None, None, None, :, None, :]
        elif reference_points.shape[-1] == 4:
            sampling_locations = reference_points[:, :, None, :, None, :2] \
                                 + sampling_offsets / self.n_points * reference_points[:, :, None, :, None, 2:] * 0.5
        else:
            raise ValueError(
                'Last dim of reference_points must be 2 or 4, but get {} instead.'.format(reference_points.shape[-1]))
        output = MSDeformAttnFunction.apply(
            value, input_spatial_shapes, input_level_start_index, sampling_locations, attention_weights, self.im2col_step)
        output = self.output_proj(output)
        return output

從架構上來看，傳統 Attention 模組通常處理一張特徵圖，但這裡支援多層特徵（不同解析度），例如 ResNet FPN 輸出的多個 stage，會被展平成一大張 input_flatten，搭配 input_spatial_shapes 和 input_level_start_index 標記每層的大小與位置。

每個 Query 自行學習偏移量
```
self.sampling_offsets = nn.Linear(d_model, n_heads * n_levels * n_points * 2)
```
這行的意思是，對於每一個 Query，模型會輸出多個 offset (dx, dy)，表示從 reference point 偏移的方向與距離，也就是「往哪看」。這些偏移點是學出來的，而非預先定義的固定格點。
Reference Points 決定「基準位置」
```
if reference_points.shape[-1] == 2:
    ...
elif reference_points.shape[-1] == 4:
    ...
```
注意力不再是 Query 對整張圖計算，而是以指定的 reference_points 為中心，在周圍偏移幾個點，做「局部加權」。這些 reference points 可以來自 Decoder query，也可以是 Encoder 特徵點的 grid 座標。

大概就這些，其他跟原本的 Attn 差異不大。

訓練策略

作者在 COCO 2017 資料集上進行實驗。

首先 Backbone 使用 ResNet-50，並且在 ImageNet 上進行預訓練。Neck 的部分直接從多尺度特徵圖中提取特徵，並且沒有使用 FPN。

可變形注意力設定：

注意力頭的數量：M = 8
每個查詢所選擇的採樣點數量：K = 4

可變形變換器編碼器中的參數在不同的特徵層之間共享。

超參數和訓練策略主要遵循 DETR 的設置，除了以下幾點：

邊界框分類採用 Focal Loss，損失權重設為 2。
將物件查詢數量從 100 增加至 300。

模型預設訓練 50 個 epoch，第 40 個 epoch 時學習率會降低為原來的 0.1 倍。使用 Adam 優化器來進行訓練，基本學習率為 $2 \times 10^{-4}$ ，且 $\beta_1 = 0.9$ ， $\beta_2 = 0.999$ ，權重衰減為 $10^{-4}$ 。

預測物件查詢參考點與採樣偏移量的線性投影的學習率會額外乘以 0.1 的縮放因子。

討論

與 DETR 的比較

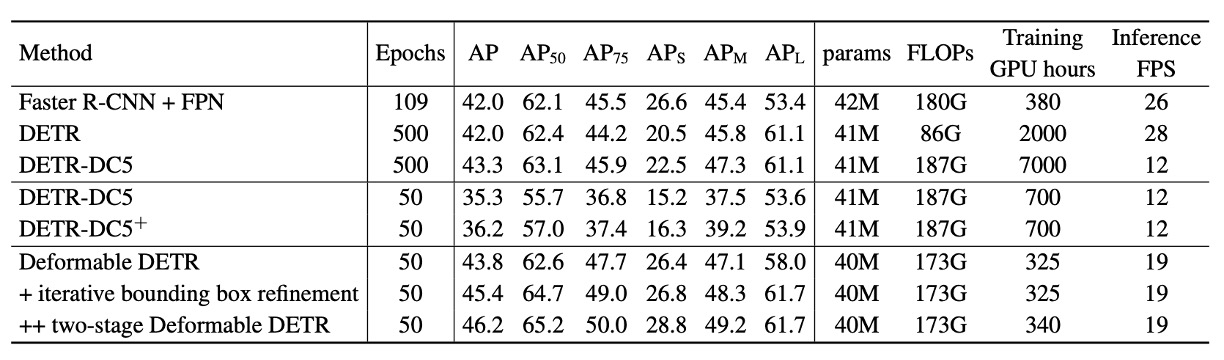
table1

根據上表，與 Faster R-CNN + FPN 相比，DETR 需要更多的訓練 epoch 才能收斂，且在小物體檢測上的表現較差。與 DETR 相比，Deformable DETR 在只需和 Faster R-CNN 相近的訓練 epoch，能夠達到更好的性能，特別是在小物體檢測方面。

詳細的收斂曲線見下圖：

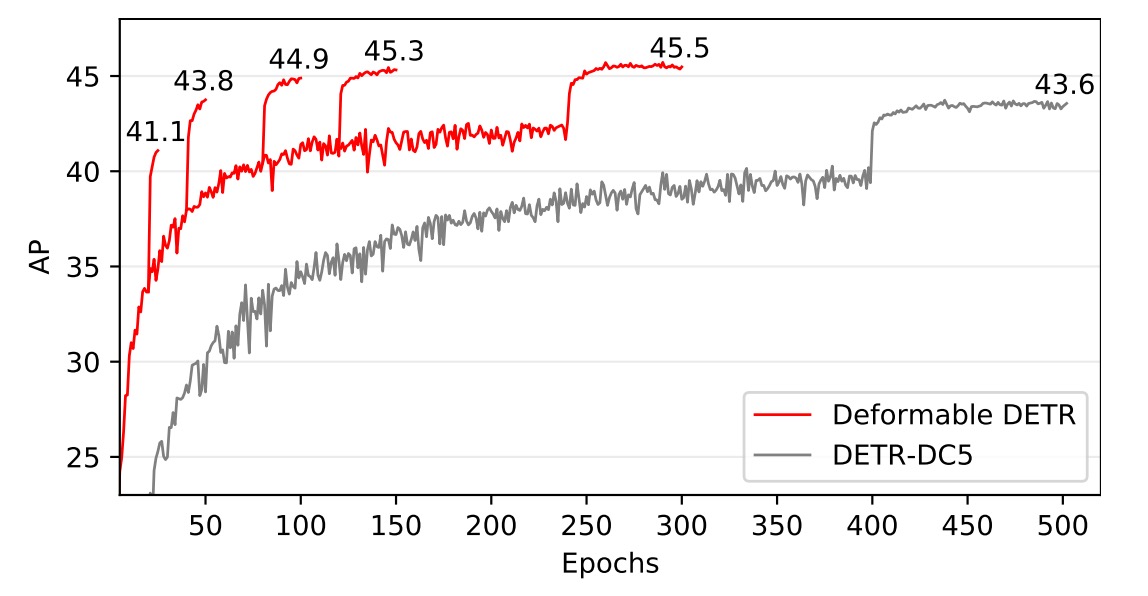
convergence

通過迭代的邊界框優化和兩階段機制，該方法進一步提升了檢測準確性。

Deformable DETR 的 FLOPs 與 Faster R-CNN + FPN 和 DETR-DC5 相當，但運行速度比 DETR-DC5 快 1.6 倍，僅比 Faster R-CNN + FPN 慢 25%。

DETR-DC5 速度較慢的原因主要在於 Transformer 注意力機制中大量的記憶體存取，而 Deformable Attention 可以緩解此問題，但代價是無序的記憶體存取，仍稍慢於傳統卷積。

消融實驗

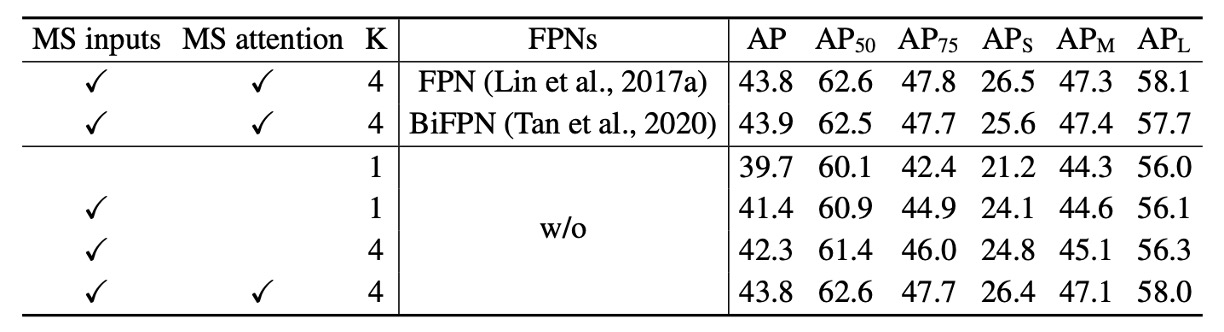
table2

上表展示了變形注意力模組中不同設計選項的消融研究。

使用多尺度輸入代替單尺度輸入能有效提升檢測準確性，平均準確度（AP）提高 1.7%，尤其是小物體檢測（APS）提高 2.9%。增加取樣點數 $K$ 可進一步提升 0.9% 的 AP。

使用多尺度變形注意力使得不同尺度層級間的信息可以交換，能額外帶來 1.5% 的 AP 提升。由於已經採用了跨層級特徵交換，加入 FPNs 並不會進一步提升性能。當未使用多尺度注意力且 $K=1$ 時，變形注意力模組退化為變形卷積，且其準確性明顯下降。

SOTA 比較

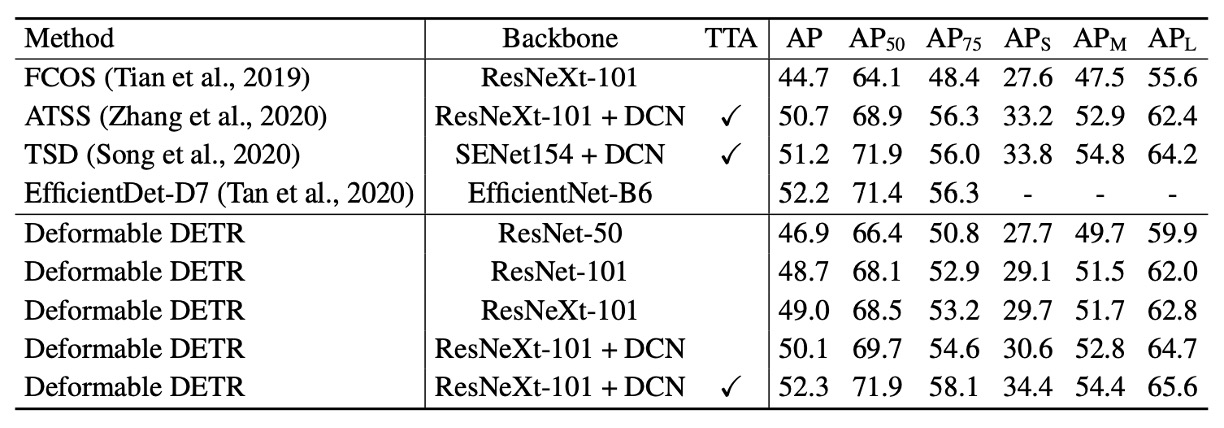
table3

在上表中，Deformable DETR 均使用了迭代邊界框優化與兩階段機制。

使用 ResNet-101 和 ResNeXt-101 時，該方法分別達到 48.7 AP 和 49.0 AP，且無需額外優化技術。使用帶有 DCN 的 ResNeXt-101 時，準確度提升至 50.1 AP。

在加入測試時增強（test-time augmentations）後，該方法達到 52.3 AP。

資訊

TTA (Test-Time Augmentations) 是一種在測試時對圖像進行多次增強，然後將多次預測的結果進行平均的技術。這樣可以提高模型的穩健性，並且提高模型的準確性。

結論

Deformable DETR 相較於傳統的 DETR，大幅縮短了訓練所需的時間。在小物體檢測的表現上，比 DETR 展現更明顯的優勢。

雖然 Deformable DETR 引入了可變形注意力以提升運行速度，但由於無序記憶體存取的特性，仍略微慢於傳統的卷積神經網路架構（如 Faster R-CNN）。因此，對於某些即時性要求高的應用，速度仍是需要考量的問題。

Deformable DETR 的設計為探索更高效、更實用的端對端物體偵測器變體開闢了新的方向，並具有廣泛的研究與應用潛力。