[18.01] MobileNet-V2

瓶頸內的淬煉

MobileNetV2: Inverted Residuals and Linear Bottlenecks

MobileNet 是一個輕量級的深度學習網路，旨在在移動設備上實現高效的圖像辨識。

在第一代 MobileNet 中，作者提出了深度可分離卷積（Depthwise Separable Convolution）的概念，以減少參數量和計算量。

在這篇論文中，作者延續了這個思路，並嘗試找到提升效能的新方法。

提示

如果你是第一次看到這篇論文，你可能會被那些噴湧而出的名詞所淹沒。

因此，這篇論文我們首要推薦看程式碼實作。

不過既然你已經點進來了，那我們就一起看一下吧。

定義問題

線性瓶頸

作者想討論的第一個問題是線性瓶頸。

假設我們有一個用於圖像辨識的深度卷積神經網路。每個卷積層都會產生一個三維的啟動張量（高度 × 寬度 × 深度），其中包含了圖像的特征。

例如，第一層可能會辨識邊緣和顏色變化，而更深的層可能會辨識更複雜的形狀或對象部分。

在神經網路的每一層中，啟動張量可以視為存在於一個高維空間中。這個空間中的有意義數據結構（在論文內稱為「興趣流形」(manifold of interest)），理論上可以被映射到一個低維子空間中，而不丟失重要信息。這是因為雖然數據在原始空間中是高維的，但它們往往圍繞某些低維結構分佈。

提示

舉個例子：如果把 128 個特徵，透過一個轉換矩陣投影到 2 維特徵中，在保有轉換資訊的前提，我們可以透過反轉換矩陣將這 2 維空間的特徵還原回 128 維空間。

為了有效利用這一性質，網路設計可以引入線性瓶頸層來降低數據的維度，這種方式在 MobileNetV1 中得到了成功應用。

然而，當引入非線性操作，如 ReLU（修正線性單元）時，情況會變得更複雜。

ReLU 的效果是對每個元素進行線性閾值處理，將所有負值設為零，這會改變數據的分佈，從而產生新的幾何結構（如射線和分段線性曲線）。

提示

延續剛才的例子：如果把 128 個特徵，透過一個轉換矩陣投影到 2 維特徵中，然後對其使用 ReLU，假設其中一個特徵值小於零，則這個特徵值會被設為零。這樣，原本的 2 維特徵空間中的點集就會被分割成兩部分，這會使得反轉換矩陣無法完全恢復原始的 128 維特徵空間。

而避免這種情況的方式，是提供足夠的維度，以便在非線性變換後仍然保留足夠的信息，如下圖所示：

在圖中，最左邊的是輸入，對於投影到不同的維度上，且經過 ReLU 運算後，右邊的分佈就會有所不同。

可以看到當我們選用的維度不夠時，經過 ReLU 運算後，原本的分佈就會被破壞，有一部分的信息將永遠丟失。

殘差網路

先看一下什麼叫做殘差網路，這裡引入 ResNet 論文內提供的圖片：

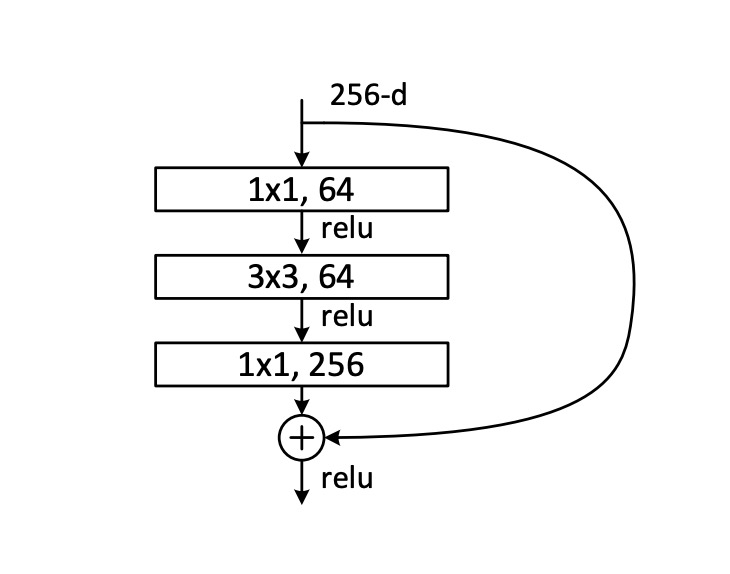
一般的殘差網路，首先經過一個 1x1 卷積層降維，然後是 3x3 卷積層彙整資訊，最後再經過一個 1x1 卷積層升維，最後再加上原始輸入。

根據剛才提到的線性瓶頸，這個殘差模組中在降維的過程中，又引入了 ReLU 的非線性運算，這樣就會丟失資訊。

資訊丟多了會怎樣？

就會導致在深層的殘差網路中的「殘差分支」失去功能，徹底淪為擺設，白白浪費了計算資源。

解決問題

為了解決問題，作者修改了原本的殘差模組，將壓縮維度改成膨脹維度，並將深度可分離卷積引入其中。

這個新的殘差模組被作者稱為「帶有線性瓶頸的反轉殘差」（Inverted residual with linear bottleneck.）。

反轉殘差

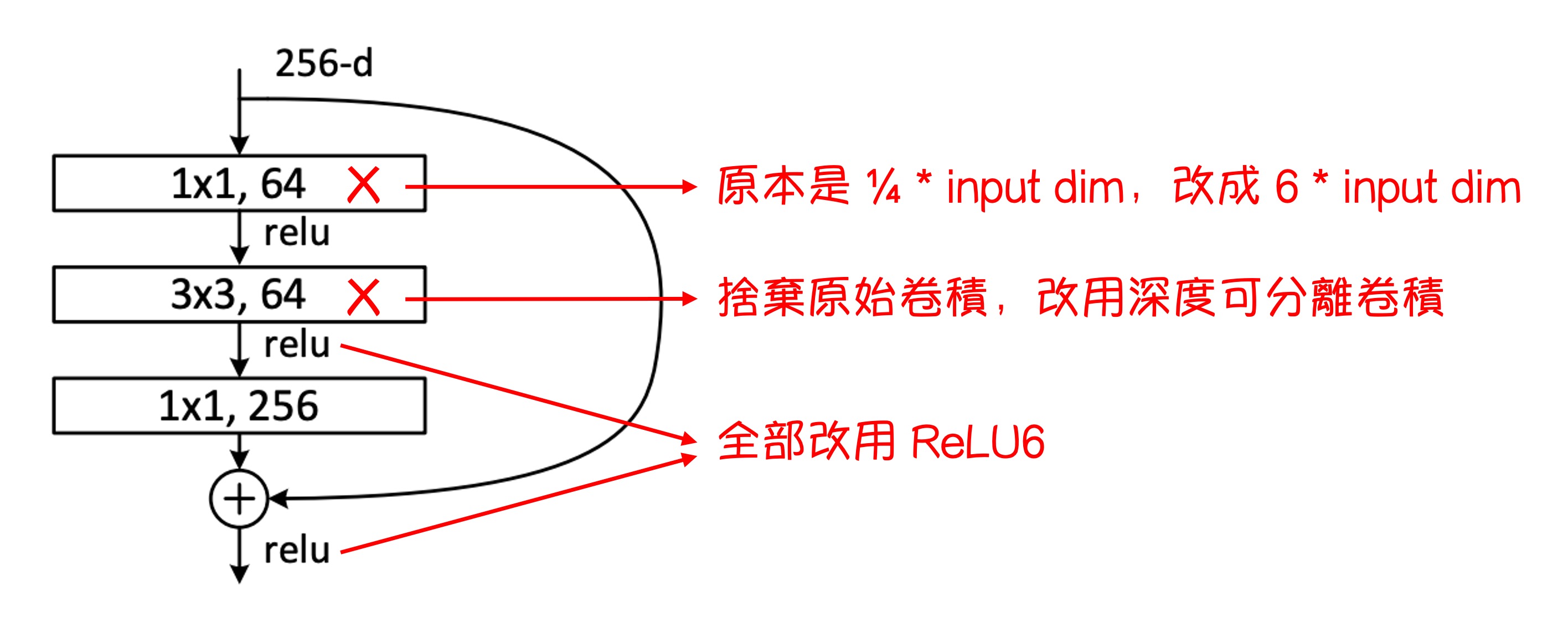
Inverted Residual

整個殘差模組的修改如上圖所示。

把原本 ResNet 中壓縮維度的 1x1 卷積層換成了擴展維度的 1x1 卷積層。
把原本 3x3 卷積層換成了深度可分離卷積。
把原本 ReLU 函數全部換成 ReLU6 函數。

提示

很抱歉，我們自己做圖顯得比較簡陋，由於論文中的很多圖其實不是那麼容易理解，這裡我們就不放了，有興趣的話可以去論文中看看。

擴張瓶頸（論文附錄 A）

瓶頸變換涉及兩個核心操作：線性變換和 ReLU 啟動函數，這一過程可以表示為 $A \text{ReLU}(Bx)$ ：

線性變換 $Bx$ ： 在此， $x \in \mathbb{R}^n$ 代表一個 n 維的向量，可以是代表圖像中的像素點的向量或是任何其他類型的數據。 $B$ 是一個 $m \times n$ 的矩陣，負責將原始的 n 維向量 $x$ 變換到 m 維空間。這一步的目的是在不同的維度上重組輸入數據的特徵，可能是為了降維（如果 $m < n$ ）、升維（如果 $m > n$ ）、或是轉換到另一個同維度的空間（如果 $m = n$ ）。
非線性啟動函數 ReLU： ReLU 函數，即修正線性單元（Rectified Linear Unit），作用於 $Bx$ 的結果。這個函數的數學表示是 $\text{ReLU}(z) = \max(0, z)$ ，其中 $z$ 可以是一個數字或一個向量。對於向量，ReLU 函數對每一元素獨立作用。這一步引入了非線性特性，有助於增加模型的表達能力，因為線性模型無法捕捉到複雜的數據結構和模式。
第二層線性變換 A： 經過 ReLU 啟動後的結果再次被一個 $n \times m$ 的矩陣 $A$ 變換。這一步可以進一步調整特徵，使其適合於後續的神經網路層或最終的輸出要求。

在分析瓶頸變換的效果時，首先要考慮 m（輸出維度）和 n（輸入維度）的關係：

當 m ≤ n 時：此類變換可能在保持非線性的同時，會有資訊損失。因為當輸出維度小於或等於輸入維度時，一些輸入信息在經過轉換後無法完全恢復。
當 n < m 時：這種變換不僅能表達強烈的非線性，而且在很大程度上是可逆的，即初始隨機權重下，轉換後的結果有很高的概率可以恢復原始輸入。

最後，作者指出擴展層的瓶頸結構不僅能防止流形崩塌（即信息喪失），還能幫助網路表示更複雜的函數。

模型架構

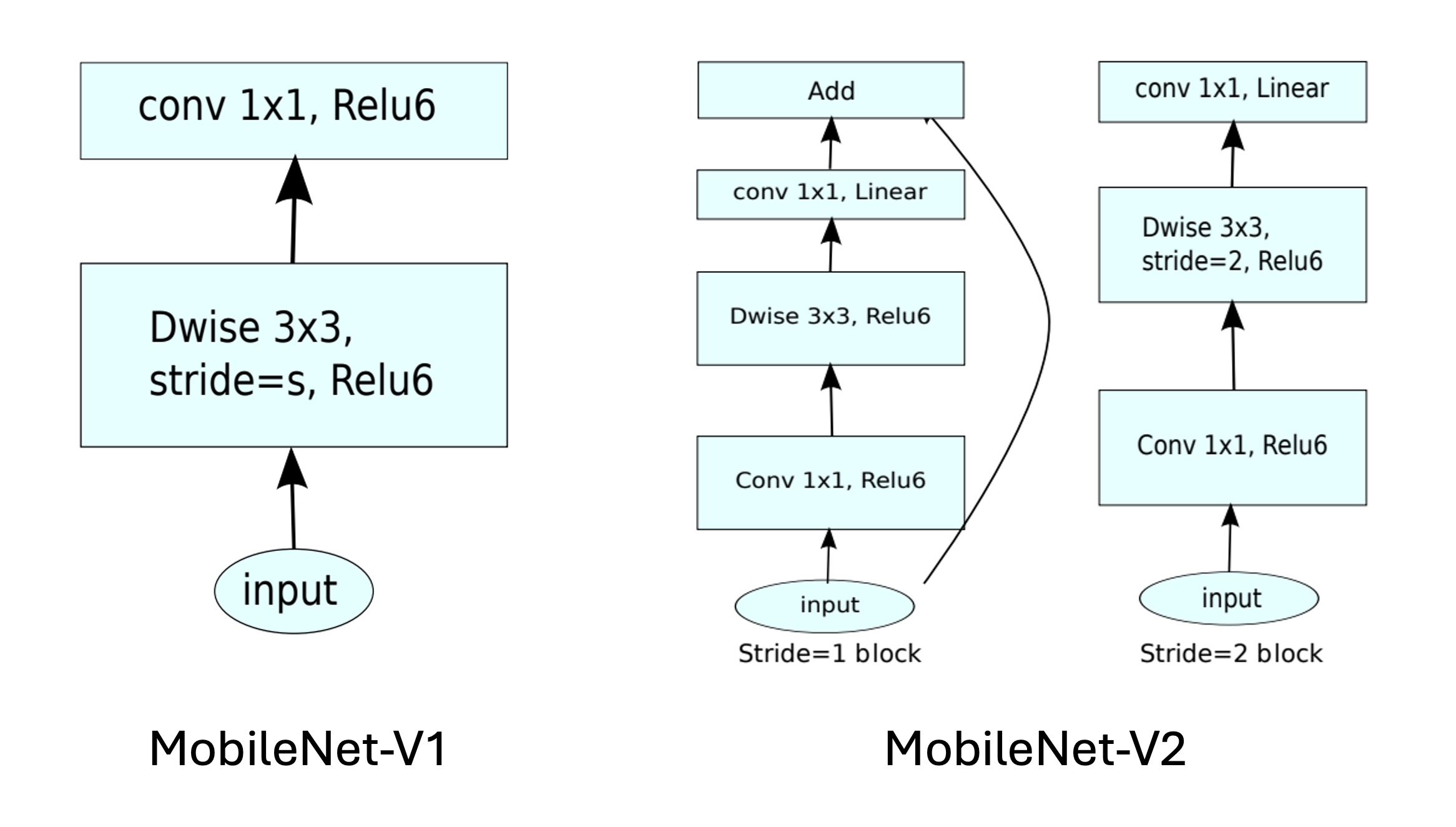
最後就是整個模型的架構，從上圖可以看到，相比於 MobileNetV1，在 MobileNetV2 中則是進一步融合殘差模組。

以下還有一點篇幅，我們直接來實作一下吧。

import torch.nn as nn


class InvertResidual(nn.Module):

    def __init__(self, inp, oup, stride, expand_ratio):
        super(InvertResidual, self).__init__()
        self.stride = stride
        self.is_shortcut = stride == 1 and inp == oup
        hidden_dim = int(inp * expand_ratio)

        self.conv = nn.Sequential(
            # pw
            nn.Conv2d(inp, hidden_dim, 1, 1, 0, bias=False),
            nn.BatchNorm2d(hidden_dim),
            nn.ReLU6(),
            # dw
            nn.Conv2d(hidden_dim, hidden_dim, 3, stride, 1, groups=hidden_dim, bias=False),
            nn.BatchNorm2d(hidden_dim),
            nn.ReLU6(),
            # pw-linear
            nn.Conv2d(hidden_dim, oup, 1, 1, 0, bias=False),
            nn.BatchNorm2d(oup),
        )

    def forward(self, x):
        if self.is_shortcut:
            return x + self.conv(x)
        else:
            return self.conv(x)

做完模組，再來就是把模型串起來。

先參考一下論文的配置：

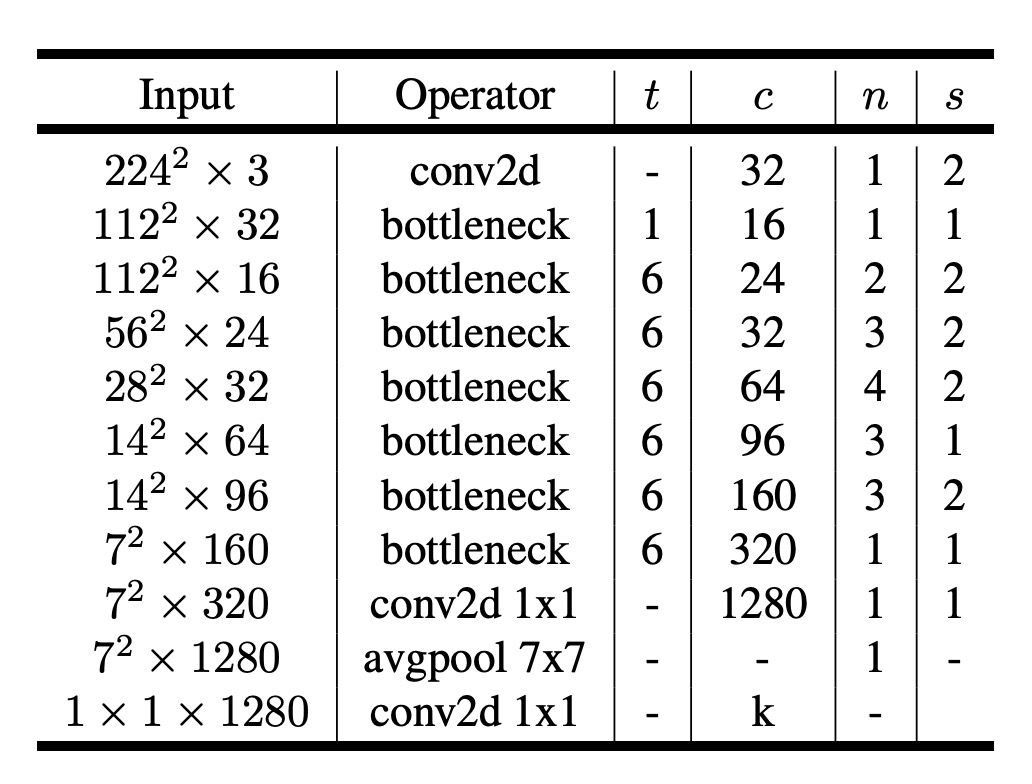
輸入圖片大小為 224x224，輸出類別數為 1000......

呃，這幾個參數不重要，不影響模型的實作。

論文中有提到需要縮放模型，因此我們需要有個可以縮放模型寬度的參數 width_mult。

這裡我們撇開最後的輸出層，只實作模型的主體部分，也就是特徵提取部分。

import torch.nn as nn

class MobileNetV2(nn.Module):

    def __init__(self, width_mult=1.):
        super(MobileNetV2, self).__init__()

        # setting of inverted residual blocks
        self.settings = [
            # t, c, n, s
            [1, 16, 1, 1],
            [6, 24, 2, 2],
            [6, 32, 3, 2],
            [6, 64, 4, 2],
            [6, 96, 3, 1],
            [6, 160, 3, 2],
            [6, 320, 1, 1],
        ]

        # building first layer
        input_channel = int(32 * width_mult)
        self.first_layer = nn.Sequential(
            nn.Conv2d(3, input_channel, 3, 2, 1, bias=False),
            nn.BatchNorm2d(oup),
            nn.ReLU6()
        )

        # building inverted residual blocks
        layers = []
        for t, c, n, s in self.settings:
            output_channel = int(c * width_mult)
            for i in range(n):
                layers.append(
                    InvertResidual(
                        input_channel,
                        output_channel,
                        stride=s if i == 0 else 1,
                        expand_ratio=t
                    )
                )
                input_channel = output_channel
        self.layers = nn.Sequential(*self.layers)

        # building last several layers
        last_channel = int(1280 * width_mult) if width_mult > 1.0 else 1280
        self.last_layer = nn.Sequential(
            nn.Conv2d(input_channel, last_channel, 1, 1, 0, bias=False),
            nn.BatchNorm2d(oup),
            nn.ReLU6()
        )

    def forward(self, x):
        x = self.first_layer(x)
        x = self.layers(x)
        x = self.last_layer(x)
        return x

提示

為什麼 nn.Conv2d 的 bias 設為 False？

因為我們在 Batch Normalization 中已經有了偏移項，因此不需要再在 Conv2d 中加入偏移項。

討論

圖像分類效能

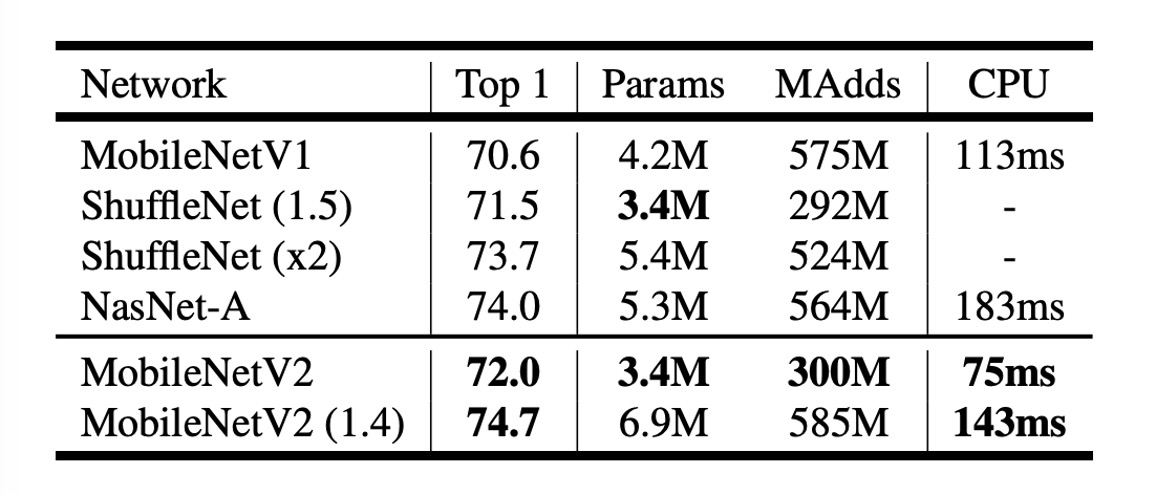
從上表可以看到，MobileNetV2 在 ImageNet 上的表現比 MobileNetV1 有所提升。

在近乎一半的計算量下，MobileNetV2 的準確率比 MobileNetV1 高了約 1.4%，推論速度提升約 30%。

在 300M 計算量的量級上，超越了幾個月前發布的 ShuffleNet。
在 600M 計算量的量級上，超越了 NASNet，同時在 CPU 的運行速度上也比 NASNet 快了約 20%。

結論

在這篇研究中，作者展示了 MobileNetV2 如何有效地應對行動設備上對高效能和低能耗的需求。

線性瓶頸層和反轉殘差模組的使用，允許模型在保持輕量級的同時，有效地管理信息流，減少信息在傳遞過程中的損失。

這種設計理念不僅提高了模型對輸入數據的表達能力，也提升了在移動裝置上的效能表現。

未來的工作將繼續探索這一架構的潛力，尋求在保持模型輕量化的同時，進一步提升效能和泛化能力。

瓶頸內的淬煉​

定義問題​

線性瓶頸​

殘差網路​

解決問題​

反轉殘差​

擴張瓶頸（論文附錄 A）​

模型架構​

討論​

圖像分類效能​

結論​