跳至主要内容

[22.01] ConvMixer

卷積混合器​

Patches Are All You Need?

這幾年常看到 「XXX is all you need」 的標題。

看到這種標題，我們就忍不住想來看看，這次又怎麼了。

定義問題​

在 ViT 提出後的近幾年，大家都想知道為什麼 Transformer 可以這麼厲害。到底是因為自注意力機制？還是因為 Token-Mixer 的機制？還是因為整個架構的設計？

在這篇論文中，作者想探討 ViT 的強大是否來自於 Patchify 的機制。於是，他們提出了 ConvMixer，目的在移除自注意力機制的影響，如果在這種的情況下，模型的性能仍然能夠保持，那麼就可以證明 Patchify 的機制「在某種程度上」是非常重要的。

解決問題​

模型架構​

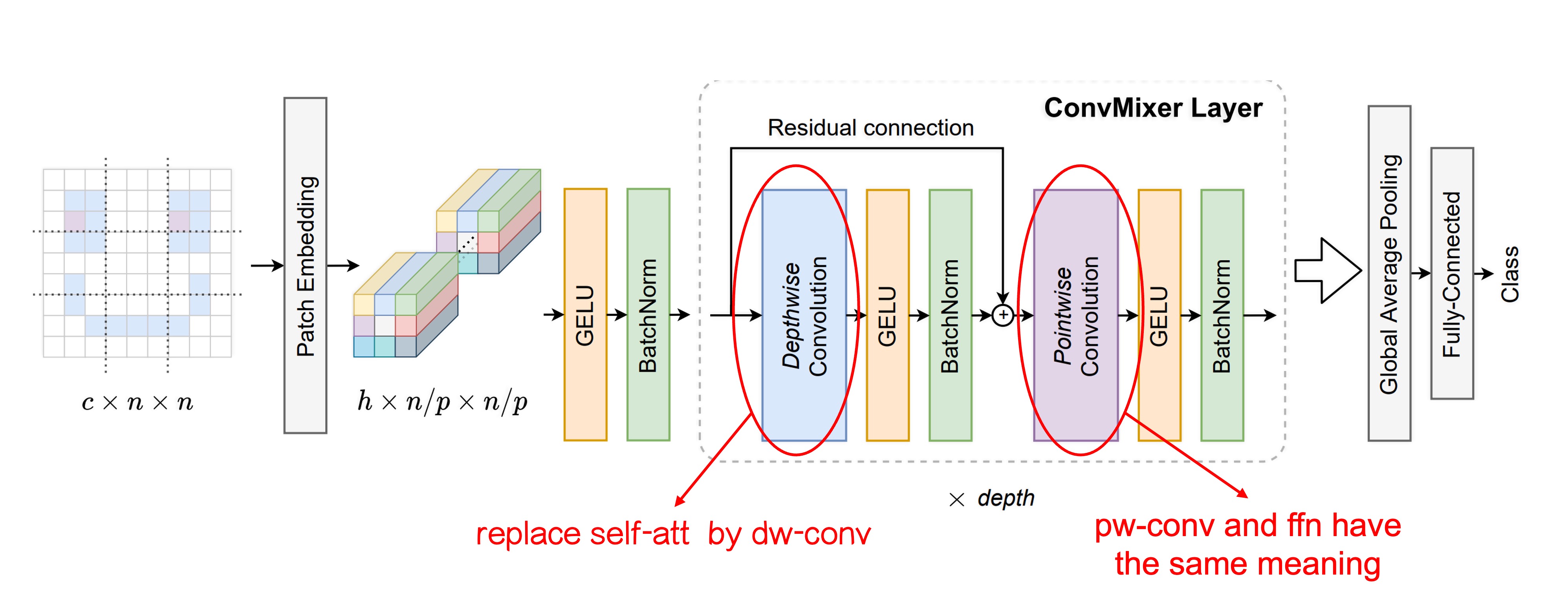
convmixer

這裡作者對原本的 ViT 架構進行改動，主要差異有兩個：

  1. 將原本的 Self-Attention 模組替換成了 Convolution 模組。

    如上圖，我們對改動的地方進行額外的標示。

    一開始的 Patchify 過程保持不變，但是在 Token-Mixer 的部分，作者將原本的 Self-Attention 模組替換成了 Depthwise Convolution。

    這樣的改動讓原本每個 Token 都可以看到其他所有的 Token，變成了每個 Token 只能看到自己「附近」的 Token（取決於卷積核的大小）。如此一來，自注意力機制就不見了，可以藉此來觀察 Patchify 的機制對於模型性能的影響。

  2. 將原本的 MLP 替換成了 Pointwise Convolution。

    這個改動其實沒改，因為 Pointwise Convolution 就是 MLP。

    會特別寫出來是因為這些操作都可以通過卷積來實現，在卷積上「針對影像通道」所做的全連接層的操作，在名稱上就叫做 Pointwise Convolution。

訓練策略​

作者沒有引入額外的訓練資料，而是直接使用 ImageNet 進行訓練。

訓練配置和其他模型差不多，使用 RandomAug、MixUp 等方法進行訓練。優化器使用 AdamW，但 Epoch 數量比較少，這部分根據論文所描述，是因為算力不足。

模型參數設計​

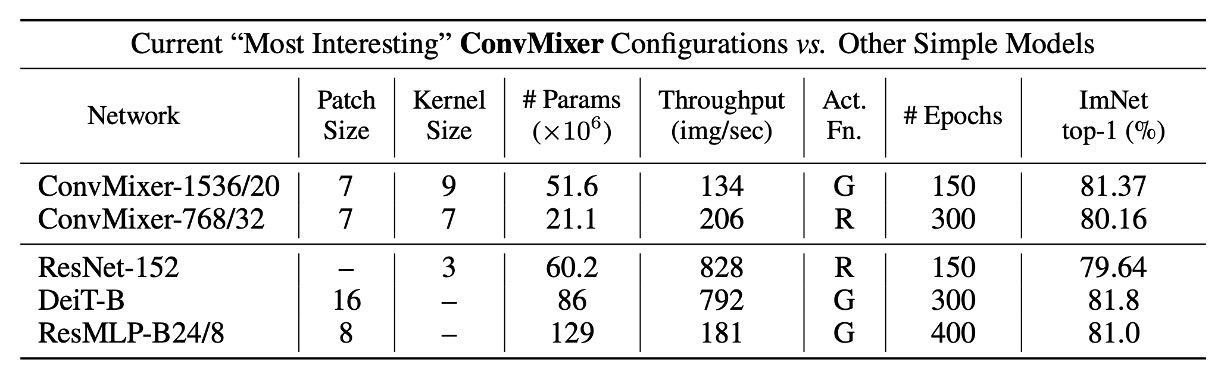
params

ConvMixer 模型的設計參數主要有以下四個：

  1. 寬度（hidden dimension, h）：即補丁嵌入的維度，也稱為模型的隱藏維度。

  2. 深度（depth, d）：ConvMixer 層的重複次數，表示模型的深度。

  3. 補丁大小（patch size, p）：控制模型內部解析度的參數。這個參數決定了輸入圖像在進行卷積時的初始劃分大小。

  4. 內核大小（kernel size, k）：深度卷積層的內核大小，影響卷積操作的範圍。

ConvMixer 模型通常依照其隱藏維度和深度來命名，例如 ConvMixer-h/d。此外，ConvMixer 支援可變大小的輸入，內部解析度則是由原始輸入大小 n 除以補丁大小 p 決定的。

討論​

在 ImageNet 上的表現​

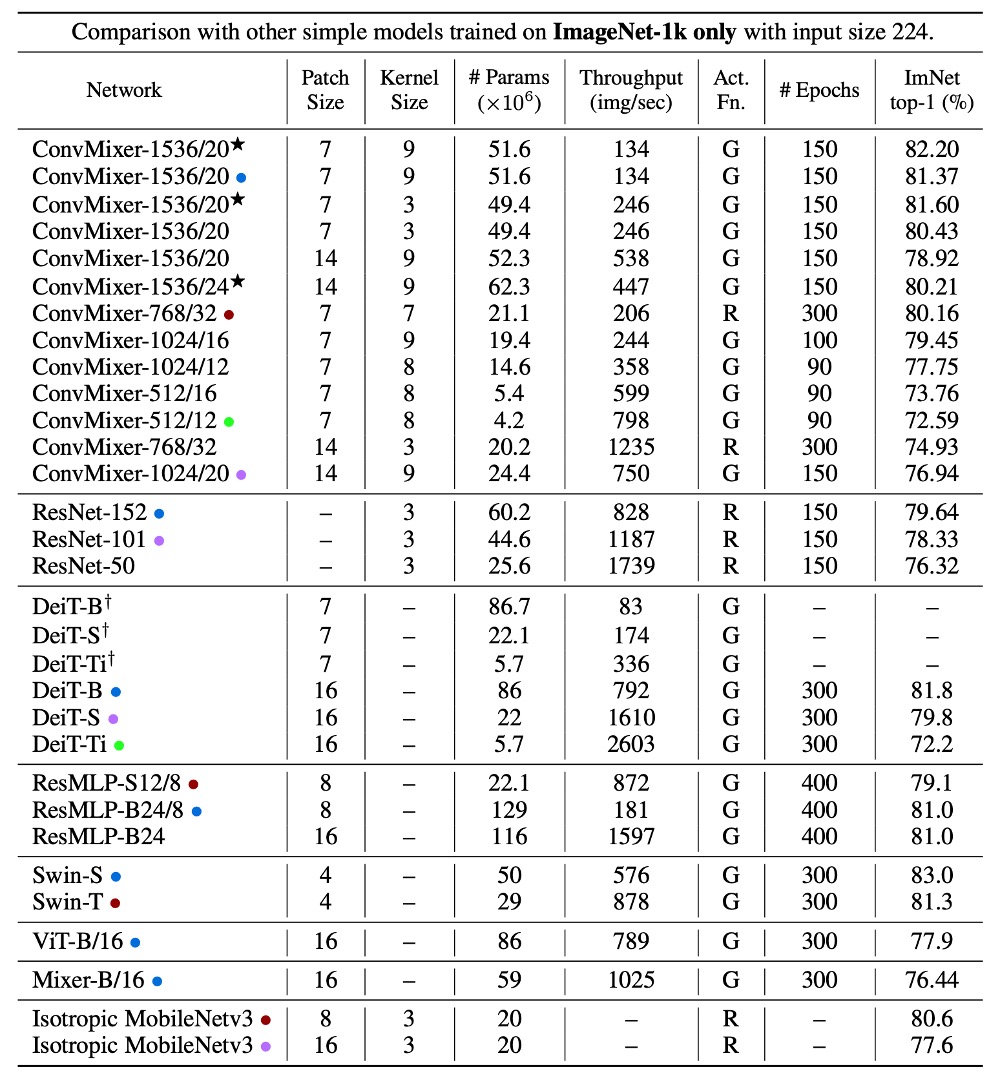
imagenet

提示

因為較小的 patch 尺寸，因此 ConvMixer 的推理速度明顯慢於其他競爭對手。

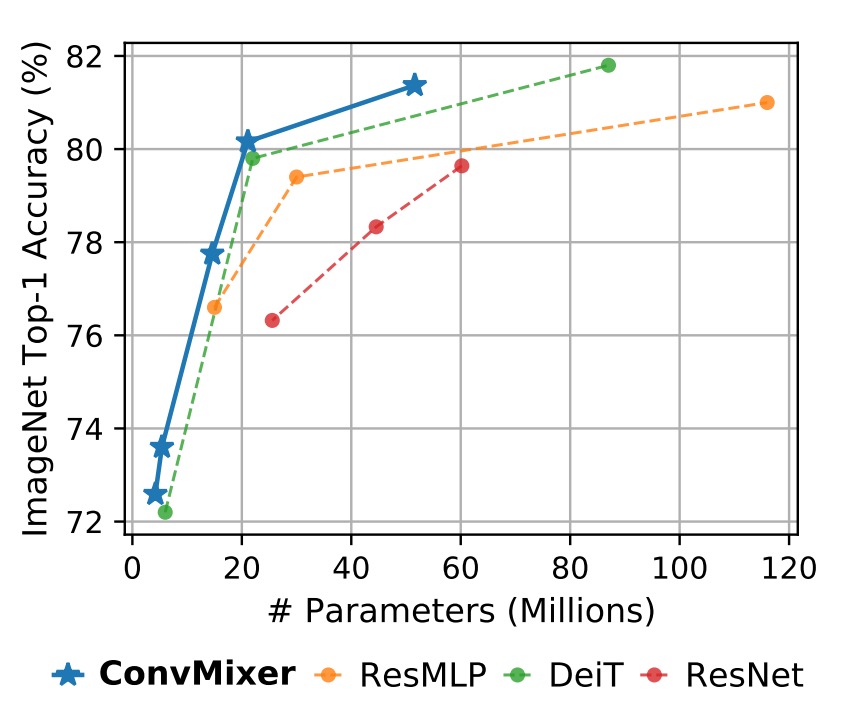
ConvMixer-1536/20 的性能優於 ResNet-152，即使其參數數量少得多。ConvMixer-768/32 在僅使用 ResNet-152 三分之一參數的情況下，也能達到類似的準確性。

ConvMixer-1536/20 儘管其參數數量相對較少，但準確性超過了 ResMLP-B24，且與 DeiT-B 的性能相當，展示了在參數數量上的高效性。相比之下，DeiT 和 ResMLP 的結果涉及超參數調整，而 ConvMixer 的結果則未進行任何超參數調整。

imagenet

結論​

這篇文章中提出了 ConvMixer 來弱化自注意力機制的影響，用於探索 Patchify 的機制。

實驗結果顯示：把自注意力機制拔掉之後，模型性能仍然能夠保持，於是作者做了兩個總結：

  1. Patchify 的機制確實是重要的。
  2. ConvMixer 的操作簡單，性能優秀，也是個值得推薦的操作。
提示

根據實驗結果，我們比較認同：「自注意力機制非必要」的結論，至於「Patchify」的部分實在太過於簡單，無法再簡化了。

大家都知道所謂的 「Patchify」，不過就是一層 Linear 操作，這其實跟 NLP 任務中常用的 nn.Embedding 操作是一樣的。在 NLP 中，我們很少會看到有人說 nn.Embedding 是一個很厲害的操作，反而大部分的精力會放在如何設計 Tokenizier，是要用 BPE 還是 WordPiece 之類的方式，把語言切割成更「高效」的 Token。

所以以這篇論文的標題來看，我們會期待看到的是一個「神奇的 Patchify」操作，可以在基於同樣的 Transformer 架構下，大幅提升模型的性能。

這時候或許我就可以說：「A good patchify is all you need」。

但這時候就又會陷入另一個兩難：

我們為了捨棄卷積網路的歸納偏差，引入了 Transformer，但卻又回過頭去幫這個更「強大」的結構加上更多的操作，彷彿我們也不信任這個「強大」的結構能夠自己解決問題。

哎呀，這個題目還真是折磨人啊！

最後由 zephyr-sh 於 更新