[21.06] LoRA

Zephyr

Dosaid maintainer, Full-Stack AI Engineer

萬分之一的 LLM

LoRA: Low-Rank Adaptation of Large Language Models

---

我們必須承認大部分的人都 Train 不了 LLM。

世界這麼大，但能夠迭代 LLM 的公司也就這麼幾家，屈指可數。

研究者們迫切地希望能夠利用這些巨大的模型來解決各種問題，所以如何有效地微調這些模型就成為了一個重要的問題。

定義問題

如果你今天想要對全模型進行微調，具體的步驟應該會像是這樣：

1. 模型首先使用預訓練權重 $\Phi_0$ 初始化。

2. 透過梯度優化更新為 $\Phi_0 + \Delta \Phi$，以最大化條件語言模型目標：

   $$\max_\Phi \sum_{(x,y) \in Z} \sum_{t=1}^{|y|} \log P_\Phi(y_t | x, y_{<t})$$

每個下游任務都需學習不同的參數 $\Delta \Phi$，且其維度 $|\Delta \Phi|$ 等於原始模型參數的大小 $|\Phi_0|$。對於大型模型，像是 GPT-3 這種的，$|\Phi_0|$ 大約有 175 億參數，儲存和部署多個微調後的模型非常困難。

在過去的研究中，主流的解題思路是 Adapter，剛好之前我們也有讀過：

• [19.02] Adapter: 參數節省九成六

但相關研究遠不止這些，這裡簡單列個幾篇，有空再來看看：

• [20.04] Exploring Versatile Generative Language Model Via Parameter-Efficient Transfer Learning
• [20.05] AdapterFusion: Non-Destructive Task Composition for Transfer Learning
• [21.04] The Power of Scale for Parameter-Efficient Prompt Tuning

只是這些方法在大規模且延遲敏感的生產場景中仍存在一定限制，因為我們還是需要增加參數量，而且有可能還會干擾原本基於平行運算部署的模型，如下表，在 GPT-2 上加入 Adapter 可以觀察到明顯的延遲增加：

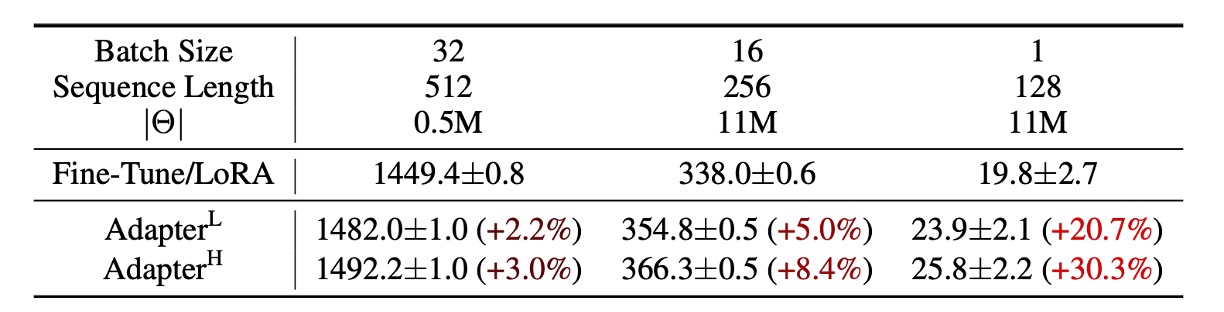
雖然可以透過層剪枝或多任務訓練來減少延遲，但無法完全消除 Adapter 的額外計算開銷。Adapter 設計本質上通過限制瓶頸維度，讓其參數量少於原始模型的 1%。

理論上計算量（FLOPs）應該不大？

但還是不行。

因為大型神經網路高度依賴硬體平行運算以保持低延遲，但 Adapter 必須順序處理，這在線上推論（batch size 通常為 1）的場景中會導致延遲顯著增加。

那不然我們改 Prefix-Tuning 呢？

• [21.01] Prefix-Tuning: Optimizing Continuous Prompts for Generation

Prefix-Tuning 等技術代表了另一種調適策略，但 prefix tuning 在優化過程中表現出非單調的參數效能變化，導致優化困難。而且為了進行調適，必須保留部分序列長度給 prefix，這減少了可用於處理下游任務的序列長度。

感覺更糟了。

作者為了解決上述的這個問題，提出了參數低秩分解的方法，將任務特定的參數增量 $\Delta \Phi$ 以較小的參數集合 $\Theta$ 編碼，且

$$|\Theta| \ll |\Phi_0|$$

目標轉換為優化較小的參數集合 $\Theta$：

$$\max_\Theta \sum_{(x,y) \in Z} \sum_{t=1}^{|y|} \log P_{\Phi_0 + \Delta \Phi(\Theta)}(y_t | x, y_{<t})$$

提示

我們保留原始論文上的數學描述，大概的意思就是找到一組參數，量級大概是原始模型的萬分之一，來代表原始模型的參數，並且在這組參數上進行微調。

但是這種參數也不是隨便就能找到，這篇論文就是要教你怎麼找。

解決問題

在開始看方法論之前，我們得先複習一下高中的數學。

秩、全秩、低秩

在數學中，矩陣 (Matrix) 是一個由數字排列而成的表格。例如：

$$\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$

矩陣在數據處理和計算中扮演了非常重要的角色，而秩 (Rank) 是衡量矩陣的關鍵指標之一。

1. 秩 (Rank) 是什麼？

   秩 (Rank) 表示一個矩陣中行向量或列向量的獨立性。

   向量的獨立性指的是：某個行（或列）不能用其他行（或列）的線性組合來表示。如果有某些行或列是彼此的組合，那麼這些行或列就不獨立。 換句話說，矩陣的秩告訴我們這個矩陣中有多少個「有用的獨立資訊」。

   如果矩陣 $A$ 是 $m \times n$ 的矩陣（即有 $m$ 行和 $n$ 列），那麼它的秩 (Rank) 是矩陣中最大獨立的行數或列數。最大秩不會超過矩陣的行數 $m$ 或列數 $n$，即

   $$\text{rank}(A) \leq \min(m, n)$$

---

2. 全秩 (Full-rank) 矩陣

   全秩矩陣是指：矩陣的秩等於行數或列數中的最小值，也就是 $\text{rank}(A) = \min(m, n)$。

   這表示矩陣中的所有行或列向量都是獨立的，沒有冗餘資訊，像是這樣：

   $$\mathbf{I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$

   這是一個 $2 \times 2$ 的矩陣，兩行向量都是獨立的。因此，它的秩為 2（等於 $\min(2, 2)$），所以這是一個全秩矩陣。每一行或列提供新的資訊，不能用其他行或列的組合來表示。

---

3. 低秩 (Low-rank) 矩陣

   低秩矩陣的秩小於其行數或列數，這表示矩陣中的部分行或列向量可以用其他行或列的組合表示，有一些冗餘資訊。這種矩陣雖然可能尺寸較大，但其中的「有用資訊」卻相對較少。

   例如，考慮以下矩陣：

   $$\mathbf{B} = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}$$

   在這個矩陣中，第二行等於第一行的 2 倍。因此，兩行向量並不獨立。這個矩陣的秩是 1（只有一個獨立向量），而非 2。因此，這是一個低秩矩陣。由於秩較低，可以用更小的矩陣來近似或描述這個矩陣。

為什麼低秩矩陣有用？

在很多應用中，我們面對的矩陣通常非常大，但其中可能有許多冗餘資訊。這時候，我們可以用低秩矩陣來近似原始矩陣，達到以下目標：

1. 減少運算成本：低秩矩陣的計算量遠小於高秩矩陣，可以加快演算法的速度。
2. 降低儲存需求：低秩矩陣所需的記憶體更少，適合處理大型資料集。
3. 資料降維：將高維度資料投影到較低的維度，仍然保留主要資訊。像是 PCA。
4. 提升模型效能：低秩矩陣可以避免模型過擬合，提高模型的泛化能力。

大家最熟悉的例子就是奇異值分解 (SVD)：它將一個矩陣拆解為幾個較小的矩陣，其中只保留最重要的資訊成分。這在圖像壓縮、推薦系統等領域非常有用。

低秩分解：LoRA

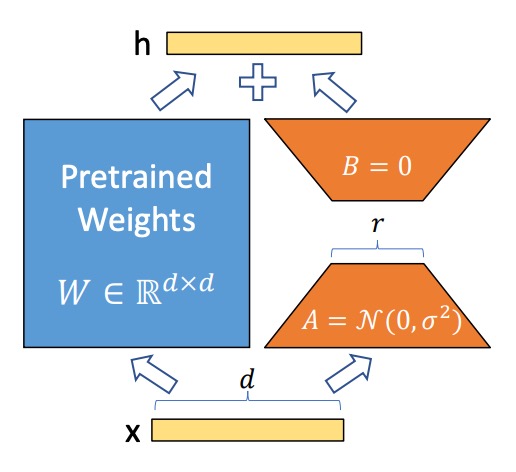
神經網路中的密集層 (Dense Layer) 使用矩陣乘法，其中的權重矩陣通常是全秩的。過去的研究指出，預訓練語言模型具有低「內在維度 (Intrinsic Dimension)」，即使被隨機投射到較小的子空間，也能維持學習效率。

• [20.12] Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning

因此，這裡作者假設在模型調適的過程中，權重的更新也具有「低內在秩」 (Low Intrinsic Rank)。即對於一個預訓練權重矩陣 $W_0 \in \mathbb{R}^{d \times k}$，作者將其更新表達為低秩分解：

$$W_0 + \Delta W = W_0 + BA$$

其中 $B \in \mathbb{R}^{d \times r}$，$A \in \mathbb{R}^{r \times k}$，且秩 $r \ll \min(d, k)$。

在訓練過程中，預訓練權重矩陣 $W_0$ 被凍結，不會更新梯度；而 $A$ 和 $B$ 則為可訓練的參數。這些矩陣會與輸入向量 $x$ 相乘，並將結果逐元素相加，公式如下：

$$h = W_0 x + \Delta W x = W_0 x + BA x$$

$A$ 使用高斯隨機分佈初始化，而 $B$ 初始為零，因此訓練開始時 $\Delta W = BA$ 為零

為了穩定性，將 $\Delta W x$ 縮放為 $\frac{\alpha}{r} \cdot \Delta W x$，其中 $\alpha$ 是與 $r$ 有關的常數。在使用 Adam 優化器時，調整 $\alpha$ 類似於調整學習率，因此可以簡化超參數調整的步驟，直接將 $\alpha$ 設為初始的 $r$ 值。

當 LoRA 的秩 $r$ 等於預訓練權重矩陣的秩時，LoRA 的表現與全模型微調接近。隨著可訓練參數增加，LoRA 的訓練效果逐漸接近原始模型。

LoRA on Transformer

LoRA 可應用於任何神經網路的權重矩陣。在 Transformer 架構中，主要針對自注意力模塊中的權重矩陣：

• 四個權重矩陣：$W_q$、$W_k$、$W_v$、$W_o$
• 每個矩陣的維度為 $d_{model} \times d_{model}$（即使其輸出常被切分成多個注意力頭）。

在本文中，作者僅針對注意力權重進行調適，並將 MLP 模組凍結以降低參數量。

這麼做帶來了幾個好處：

• 減少記憶體與存儲需求：在大型 Transformer 模型（如 GPT-3 175B）上：
  • VRAM 使用量從 1.2TB 降至 350GB（若 $r \ll d_{model}$）。
  • 若 $r = 4$，且僅調整查詢和數值投影矩陣，檢查點大小從 350GB 減少至 35MB（約 10,000 倍縮減）。
• 減少 GPU 使用與避免 I/O 瓶頸：儲存需求降低後，可用更少的 GPU 訓練。
• 快速切換任務：僅需交換 LoRA 權重即可切換任務，無需重新加載整個模型。
• 加速訓練：相比全模型微調，LoRA 在 GPT-3 175B 上訓練速度提升約 25%，因為大多數參數無需計算梯度。

但也不是完全沒有缺點，若將 $A$ 和 $B$ 吸收到 $W$ 中以消除推論延遲，不同任務的批次輸入將變得困難。在某些延遲不敏感的場景中，可選擇不合併權重，並動態挑選對應的 LoRA 模組來處理不同的批次輸入。

提示

這裡其實就是重參數化的概念，意思是另外一組參數會外掛在原本模型外，必要時刻可以直接融合進原本的模型，但會造成一些不良的影響。

所以在推論速度不是問題的情況下，可以選擇不合併權重，這樣就可以動態挑選對應的 LoRA 模組來處理不同的批次輸入。

討論

實驗基準

作者在 RoBERTa、DeBERTa、GPT-2 和 GPT-3 上進行了實驗，以下定了幾個基準：

1. 微調 (Fine-Tuning, FT)

   • 全模型微調：從預訓練權重與偏置初始化，並更新所有參數的梯度。
   • 部分層微調 (FTTop2)：僅更新 GPT-2 的最後兩層參數 (Li & Liang, 2021)。
   • 偏置微調 (BitFit)：僅訓練偏置向量，其餘參數保持凍結 (Zaken et al., 2021)。

---

2. 提示嵌入調整 (Prefix-Embedding Tuning, PreEmbed)

   在輸入 token 之間插入特殊 token，這些 token 具有可訓練的詞嵌入。

   • 策略：
     • 前綴 (Prefix)：在提示詞前加入特殊 token。
     • 中綴 (Infix)：在提示詞後加入特殊 token。
   • 參數數量： $$|\Theta| = d_{model} \times (l_p + l_i)$$ 其中 $l_p$ 和 $l_i$ 分別是前綴與中綴的 token 數。

---

3. 提示層調整 (Prefix-Layer Tuning, PreLayer)

   不僅調整詞嵌入，而是為每一層 Transformer 層學習對應的激活值。

   • 參數數量： $$|\Theta| = L \times d_{model} \times (l_p + l_i)$$ 其中 $L$ 為 Transformer 的層數。

---

4. 適配層微調 (Adapter Tuning)

   • AdapterH：原始設計 (Houlsby et al., 2019)，將適配層插入於自注意力模塊與殘差連接之間。
   • AdapterL：僅在 MLP 模塊後與 LayerNorm 後應用 (Lin et al., 2020)。
   • AdapterP：與 AdapterL 類似 (Pfeiffer et al., 2021)。
   • AdapterD：移除部分適配層以提升效率 (Rücklé et al., 2020)。
   • 參數數量： $$|\Theta| = \hat{L}_{Adpt} \times (2 \times d_{model} \times r + r + d_{model}) + 2 \times \hat{L}_{LN} \times d_{model}$$ 其中 $\hat{L}_{Adpt}$ 為適配層數量，$\hat{L}_{LN}$ 為可訓練的 LayerNorm 數量。

---

5. LoRA 調適 (LoRA Tuning)

   在原始權重矩陣旁加入低秩分解矩陣進行更新，並與原始權重矩陣平行運算。大部分實驗中，僅對查詢矩陣 $W_q$ 與數值矩陣 $W_v$ 應用 LoRA。

   • 參數數量：

     $$|\Theta| = 2 \times \hat{L}_{LoRA} \times d_{model} \times r$$

     其中 $\hat{L}_{LoRA}$ 為應用 LoRA 的權重矩陣數量，$r$ 為秩。

和其他微調方法的比較

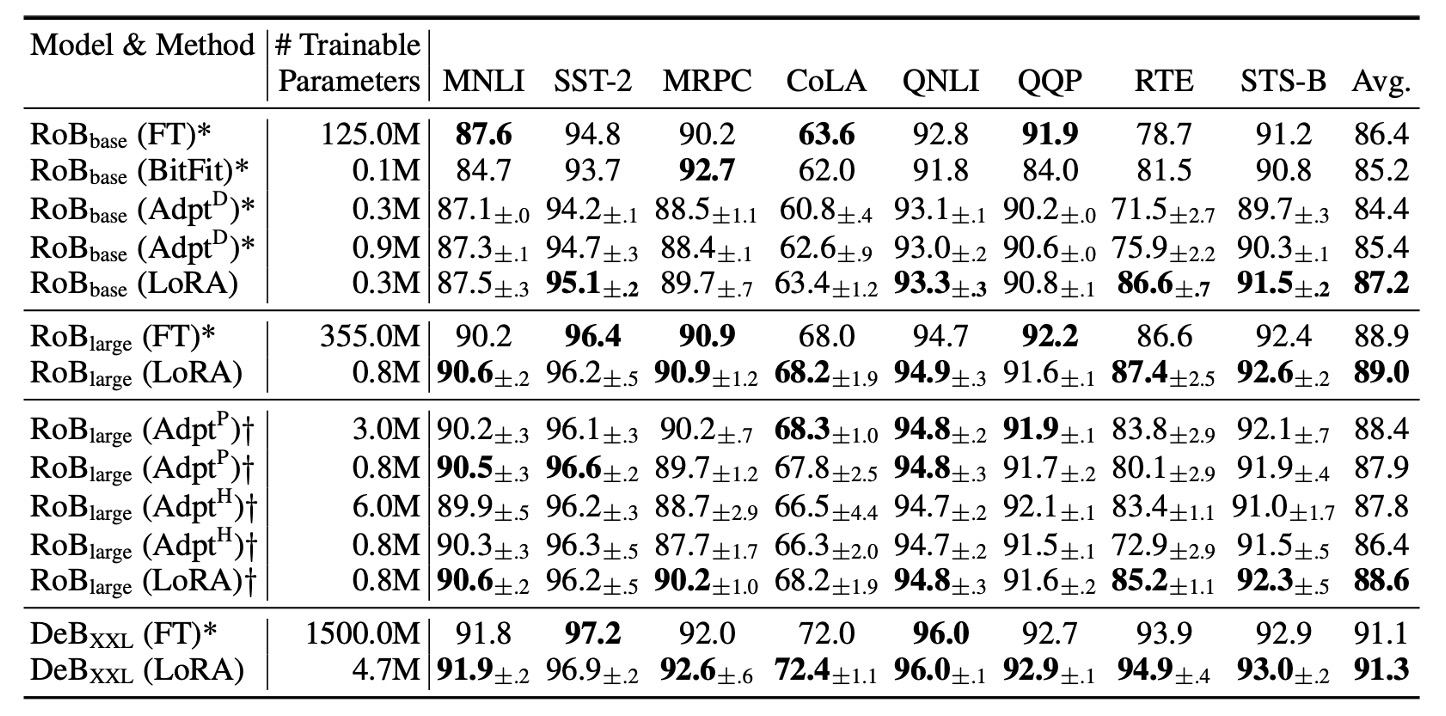
作者從 HuggingFace 中取得 RoBERTa Base (125M) 和 RoBERTa Large (355M) 進行測試。

提示

什麼是 RoBERTa？

RoBERTa 是基於 BERT 的模型，通過對 BERT 的訓練過程進行了一系列的優化，提高了模型的性能。我們之前有讀過：

• [19.07] RoBERTa: 訓練 BERT 的說明書

為了與 Adapter 基準進行公平比較，做了以下兩項調整：

1. 相同的批次大小與序列長度：所有任務使用相同的批次大小，序列長度設為 128，以符合適配層的基準設置。
2. 模型初始化方式：針對 MRPC、RTE 和 STS-B 任務，是從預訓練模型初始化，而非像微調基準一樣從已適應 MNLI 的模型開始。

實驗結果如上表，LoRA 在 RoBERTa Base 和 RoBERTa Large 上的表現接近全模型微調，並且在大多數任務上優於 Adapter 和其他高效調適方法。

DeBERTa 是 BERT 的一個更近期的變體，訓練規模更大，在 GLUE 和 SuperGLUE 等基準上表現極具競爭力。作者在 DeBERTa 上進行了 LoRA 的實驗，結果如上表最底層所示。LoRA 大多數表現都超越全模型微調。

微調 GPT-3

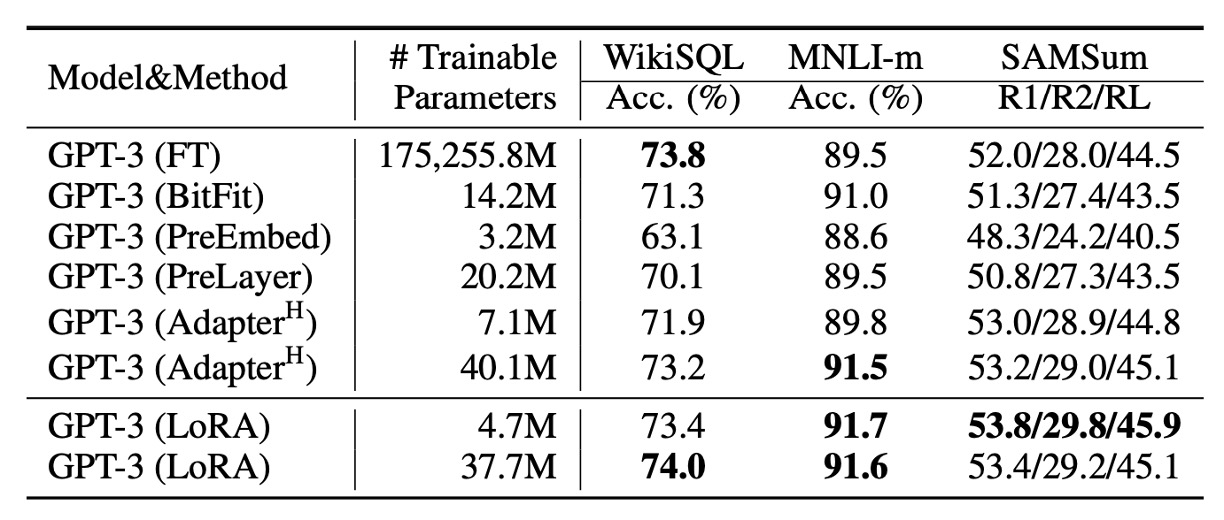
最後，終於來到微調 GPT-3 的部分了！

實驗結果如上表，LoRA 全面超越了 Adapter 和其他高效調適方法。

除此之外，也不是所有方法在增加可訓練參數時都能單調提升效能，如下圖所示：

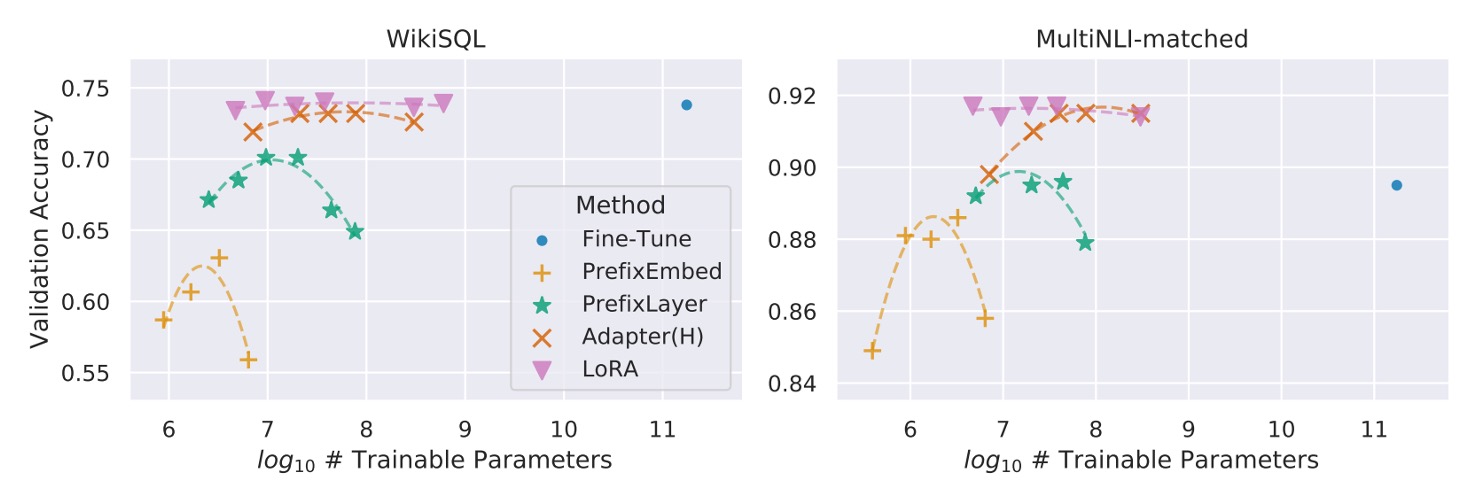
Prefix-embedding tuning 使用超過 256 個特殊 token 時，效能明顯下降。Prefix-layer tuning 使用超過 32 個特殊 token 時，亦出現效能衰退。這種現象可能是由於特殊 token 數量過多，導致輸入分佈偏離預訓練資料的分佈。

在 Transformer 中應該對哪些權重矩陣應用 LoRA？

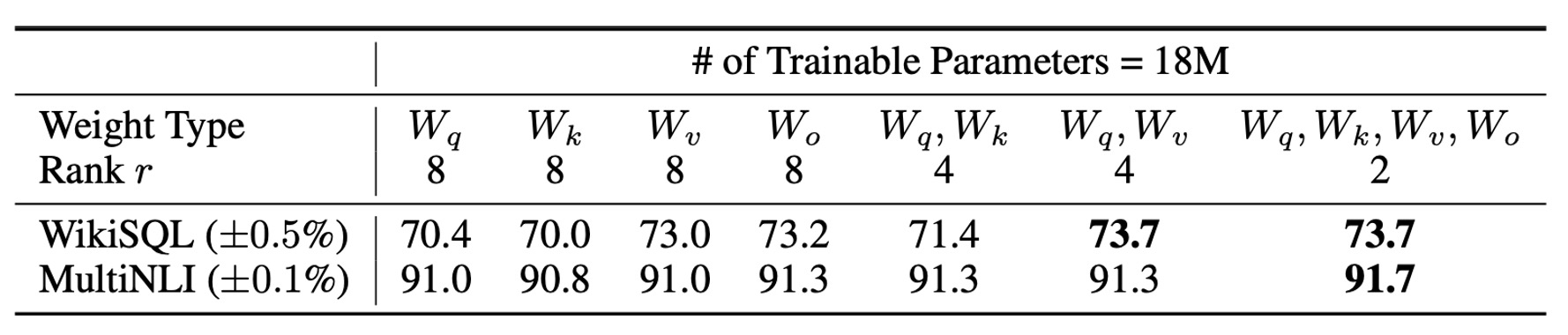
在有限的參數預算下，應該調適哪些類型的權重矩陣，才能在下游任務中獲得最佳性能？

作者基於 GPT-3 175B 進行相關實驗，在 GPT-3 175B 上設定為 1800 萬參數（約 35MB，若以 FP16 儲存）。對於所有 96 層，若調適一種類型的注意力權重，則秩 $r = 8$；若調適兩種類型，則 $r = 4$。

結果如上表：

• 僅調適 $\Delta W_q$ 或 $\Delta W_k$：性能顯著下降。
• 同時調適 $W_q$ 和 $W_v$：取得最佳結果。

即使秩 $r = 4$，$\Delta W$ 也能捕捉足夠的信息。意思就是調適更多種類的權重矩陣，並使用較小的秩，比僅調適單一類型的權重且使用較大的秩更為有效。

LoRA 的最佳秩 $r$ 是多少？

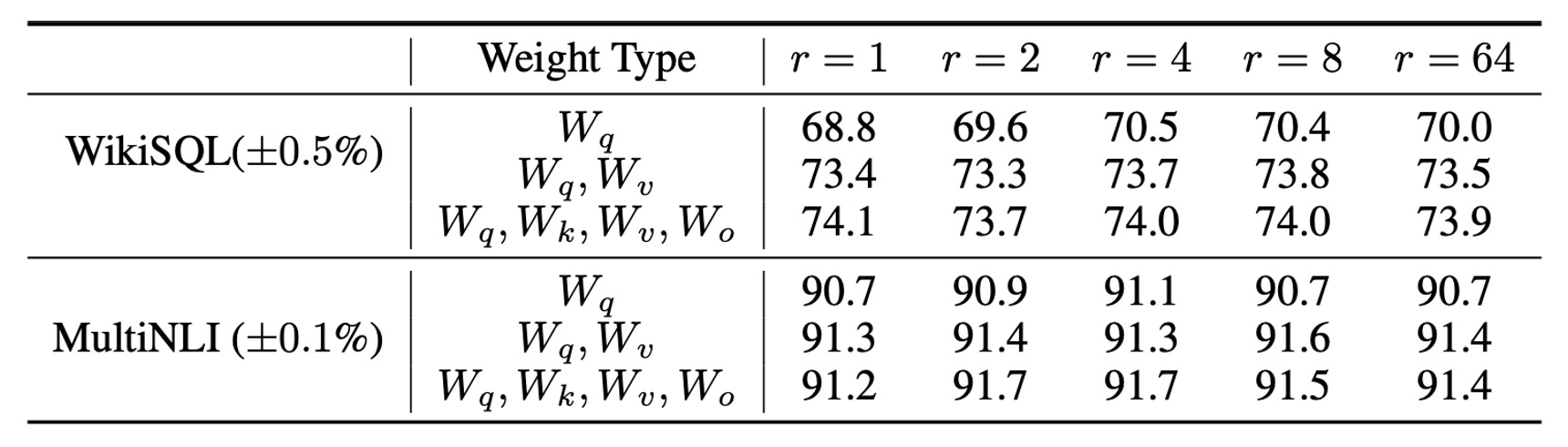
LoRA 在非常小的秩 $r$ 下已能取得優異表現，特別是調適 $\{W_q, W_v\}$ 時。

增加 $r$ 並未涵蓋更多有意義的子空間，這表明低秩的適應矩陣已足夠。

子空間相似性分析

作者想知道在不同 $r$ 值之間的子空間相似性，以及不同隨機種子之間的子空間相似性。這裡採用的方法是對這些矩陣進行奇異值分解（SVD），得到右奇異矩陣：

$$U_{A_{r=8}} \quad \text{和} \quad U_{A_{r=64}}$$

作者的目標是想知道：$U_{A_{r=8}}$ 的前 $i$ 個奇異向量形成的子空間，有多少包含在 $U_{A_{r=64}}$ 的前 $j$ 個奇異向量形成的子空間中？

計算相似度的方式是基於 Grassmann 距離的歸一化子空間相似度：

$$\phi(A_{r=8}, A_{r=64}, i, j) = \frac{\left\| U_{A_{r=8}}^{i^\top} U_{A_{r=64}}^{j} \right\|_F^2}{\min(i, j)} \in [0, 1]$$

其中 $U_{A_{r=8}}^{i}$ 表示 $U_{A_{r=8}}$ 的前 $i$ 個奇異向量的列。

結果如下圖：

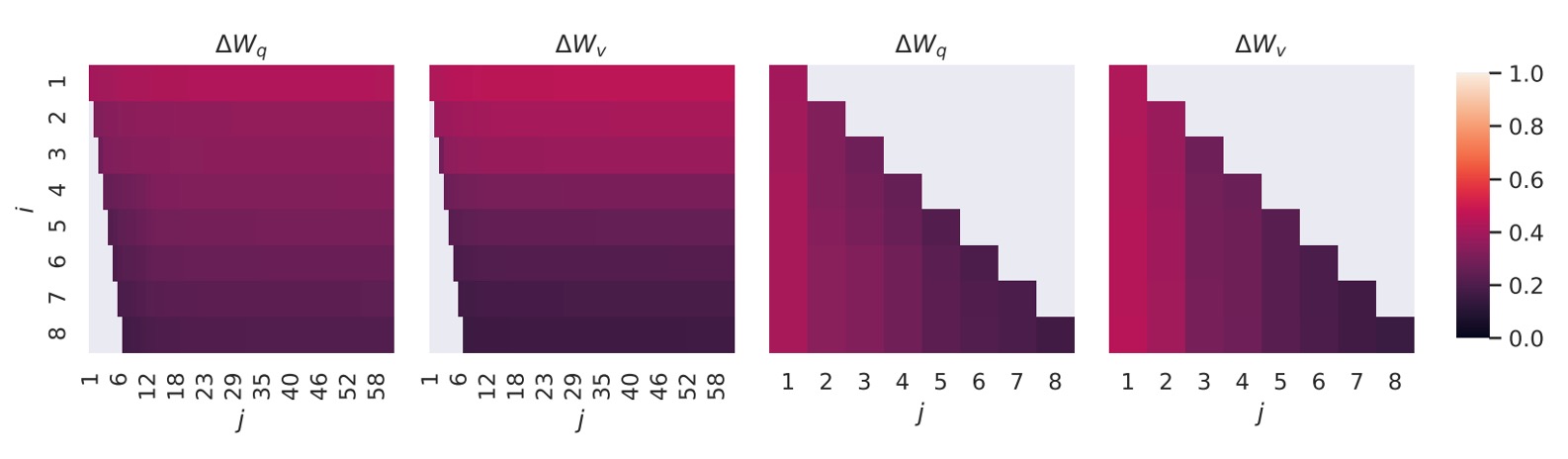
頂層奇異向量的方向在 $A_{r=8}$ 和 $A_{r=64}$ 之間高度重疊，而其他方向則重疊較少。整體看來，$A_{r=8}$ 和 $A_{r=64}$ 的 $\Delta W_v$（或 $\Delta W_q$）共享一個維度的子空間，且相似度 $\phi > 0.5$。

這說明了為何在下游任務中，秩 $r = 1$ 也能取得不錯的效果，因為最有用的信息集中在頂層奇異向量中。

---

最後彙整一下作者在論文中提出的幾個觀點：

1. 低秩適應矩陣已足夠：即使秩 $r$ 非常小，LoRA 仍能在下游任務中取得與全模型微調相當的性能。
2. 適應更多權重矩陣比提高秩更有效：在有限的參數預算下，優先調適更多類型的權重矩陣（如同時調適 $W_q$ 和 $W_v$），即使使用較小的秩，也能提升性能。

結論

與其他微調的方法相比之下，LoRA 給得實在太多了！

它顯著地（10000 倍！）減少了可訓練參數數量，並且保留了模型的完整表現：

• 我們終於也可以一起來微調 LLM 了！

在 2021 年的這個時刻，全民微調 LLM 已經不再是一個夢想，而是一個可以實現的目標。這表示我們可以讓大模型的效能深入到更多應用中，並且在更多場景下發揮其優勢。

未來十年可能都會非常熱鬧，我們可以期待更多有趣的研究成果！