[15.06] YOLO-V1

一度見るだけで

You Only Look Once: Unified, Real-Time Object Detection

---

物体検出システムでは、通常、全体のプロセスを 2 つの主要なステップに分割します：領域提案（region proposal）と分類。

1. 領域提案：

   このステップの目的は、潜在的な物体候補ボックスを生成することです。

   例えば、R-CNN は選択的検索（Selective Search）を使用して数千の候補領域を生成します。さらに進んだ方法である Faster R-CNN は、領域提案ネットワーク（RPN）を使用してこれらの候補ボックスを生成し、このプロセスをエンドツーエンドで最適化しようとします。これにより効率は向上しますが、依然として画像に対して何度もニューラルネットワークを実行する必要があります。

2. 分類：

   領域提案の後、分類器は各候補ボックスを個別に処理し、その中の物体のクラスを判別します。例えば、R-CNN では、畳み込みニューラルネットワーク（CNN）が各候補領域から特徴を抽出し、その後サポートベクターマシン（SVM）を使用して分類します。この個別処理は精度の面で一定の利点がありますが、各候補領域を個別に処理するため、速度が遅くなります。

問題の定義

上記のプロセスの主な問題は、その処理速度にあります。各候補領域ごとに特徴を抽出し分類する必要があり、これにより膨大な計算量と時間が消費されます。これこそが本論文で解決しようとする核心的な問題です：物体を検出するために、システムが画像を一度見るだけでよいのか？

YOLO は、物体検出問題を単一の回帰問題として再定義することによって、入力画像のピクセルから直接境界ボックスの座標とクラス確率を予測します。この方法の主な利点は以下の通りです：

• 一度の処理：YOLO のニューラルネットワークは、1 回の前方伝播で物体検出の全過程を完了でき、画像を何度も処理する必要がなくなります。これにより、検出速度が大幅に向上し、検出プロセスが簡素化されます。
• 全体推論：YOLO は訓練と予測の際に画像全体を考慮するため、全体のコンテキスト情報を活用して検出精度を向上させます。
• リアルタイム性能：YOLO モデルの設計は、速度と精度の間で良好なバランスを実現しており、リアルタイムでの検出が可能です。

YOLO の設計は、元々の性能を維持しながら、より速い検出速度を実現しています。これにより、非常に実用的な物体検出方法となっています。

解決される問題

モデルアーキテクチャ

ヒント

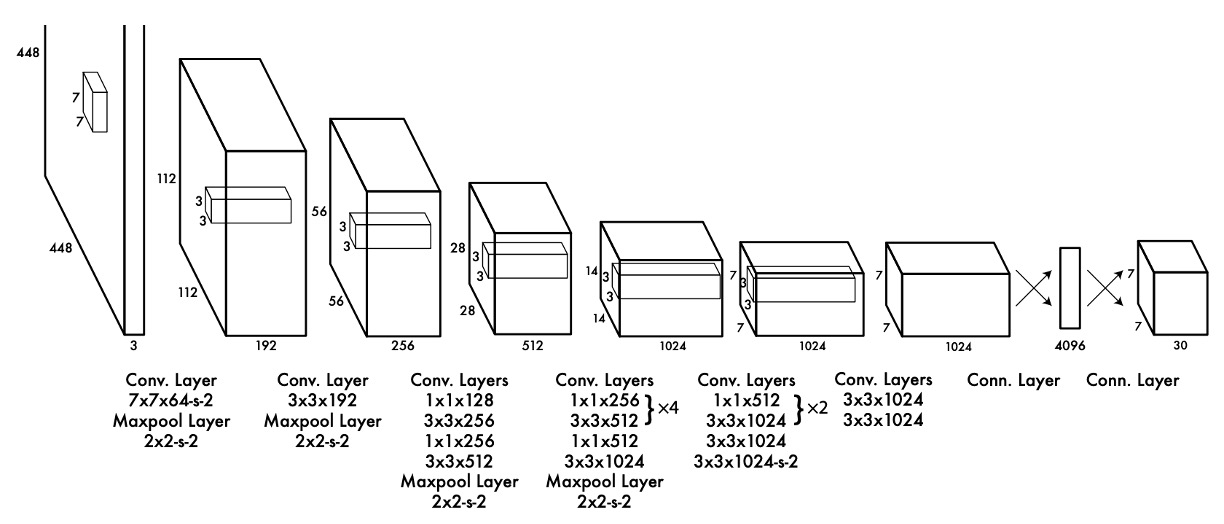
この切り取られたように見える画像は、AlexNet への敬意を表しているのではないかと考えられます。

---

領域提案と分類システムを統合するために、著者は上記のモデルアーキテクチャを提案しました。

バックボーンを通した後、最後の層の特徴マップを取り出し、次に全結合層を通過させます。

実際、バックボーンにはどんなモデルでも使用できますが、著者は論文の中で Darknet-19 を使用したと述べています。これは著者が独自に設計したネットワークアーキテクチャで、速さと精度を求めています。

全結合層の役割は特徴マップの情報を統合し、次に予測結果を予測ヘッドに投影することです。

この予測ヘッドは著者によって慎重に設計されており、上の図のように予測ヘッドのサイズは 7x7x30 です。ここでの 7x7 は、予測ヘッドが元の画像サイズに対応して 7x7 のグリッドに分割されていることを示しています。以下の図を参照してください：

---

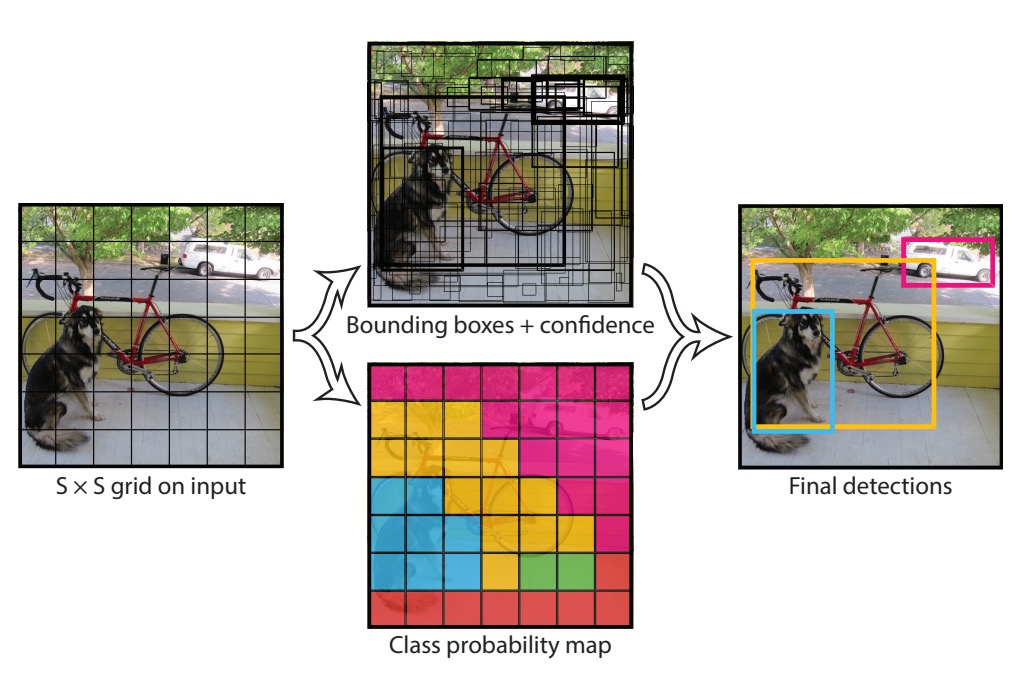
各グリッドは以下のことを行います：

1. 2 つの境界ボックスを予測：各ボックスは物体の位置に対応し、形式は(x, y, w, h)です。ここで、(x, y)はグリッドの中心、wとhは物体の幅と高さです。
2. 物体のクラスを予測：著者は 20 種類の物体を使用しているため、各グリッドは 20 個のクラスを予測します。

したがって、論文ではいくつかのハイパーパラメータが設定されています：

1. S: 各辺に何個のグリッドがあるか。ここでは 7 です。
2. B: 各グリッドが予測する境界ボックスの数。ここでは 2 です。
3. C: クラスの数。ここでは 20 です。

損失関数

この予測結果には大量のオーバーラップがあるに違いありません。

次に著者は損失関数を提案し、この損失関数は複数の部分で構成されています：

$$λ_{coord} \sum_{i=0}^{S^2} \sum_{j=0}^{B} 1_{obj}^{ij} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 \right]$$ $$+ λ_{coord} \sum_{i=0}^{S^2} \sum_{j=0}^{B} 1_{obj}^{ij} \left[ \left( \sqrt{w_i} - \sqrt{\hat{w}_i} \right)^2 + \left( \sqrt{h_i} - \sqrt{\hat{h}_i} \right)^2 \right]$$ $$+ \sum_{i=0}^{S^2} \sum_{j=0}^{B} 1_{obj}^{ij} \left( C_i - \hat{C}_i \right)^2$$ $$+ λ_{noobj} \sum_{i=0}^{S^2} \sum_{j=0}^{B} 1_{noobj}^{ij} \left( C_i - \hat{C}_i \right)^2$$ $$+ \sum_{i=0}^{S^2} 1_{obj}^{i} \sum_{c \in \text{classes}} \left( p_i(c) - \hat{p}_i(c) \right)^2$$

---

この損失関数は 5 つの主要な部分で構成されており、それぞれの部分がモデルの予測に異なる貢献をしています：

1. 座標損失（Coordinate Loss）

   $$λ_{coord} \sum_{i=0}^{S^2} \sum_{j=0}^{B} 1_{obj}^{ij} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 \right]$$

   この部分の損失は、予測された境界ボックスの中心点（$x$ と $y$）と真の値との違いを測定します。$λ_{coord}$は重み係数で、座標損失が全体の損失関数に与える影響を調整します。指示関数$1_{obj}^{ij}$は、セル$i$と境界ボックス$j$が物体を含んでいる場合にのみ、この損失を計算することを示します。

2. サイズ損失（Size Loss）

   $$λ_{coord} \sum_{i=0}^{S^2} \sum_{j=0}^{B} 1_{obj}^{ij} \left[ \left( \sqrt{w_i} - \sqrt{\hat{w}_i} \right)^2 + \left( \sqrt{h_i} - \sqrt{\hat{h}_i} \right)^2 \right]$$

   この部分の損失は、予測された境界ボックスの幅（$w$）と高さ（$h$）との違いを測定します。平方根を使用するのは、大きな境界ボックスと小さな境界ボックスとの間で損失の差異を減少させるためです。これにより、大きなボックスと小さなボックスが損失においてより均等に扱われます。重み係数と指示関数は座標損失と同様です。

   ヒント

   平方根がどう関係しているのか？

   例えば、2 つの境界ボックスの予測と真実が以下の通りだとします：

   1. 小さな境界ボックス：

      • 真実値：$w = 2$, $h = 2$

      • 予測値：$\hat{w} = 3$, $\hat{h} = 3$

   2. 大きな境界ボックス：

      • 真実値：$w = 200$, $h = 200$

      • 予測値：$\hat{w} = 300$, $\hat{h} = 300$

   平方根を使用しない場合、サイズ損失（幅のみ考慮）は次のようになります：

   $$\text{小さな境界ボックス損失} = (w - \hat{w})^2 = (2 - 3)^2 = 1$$$$\text{大きな境界ボックス損失} = (w - \hat{w})^2 = (200 - 300)^2 = 10000$$

   大きな境界ボックスの損失は、小さな境界ボックスの損失よりも遥かに大きいことがわかります。

   平方根を使用した場合、サイズ損失（幅のみ考慮）は次のようになります：

   $$\text{小さな境界ボックス損失} = (\sqrt{w} - \sqrt{\hat{w}})^2 = (\sqrt{2} - \sqrt{3})^2 \approx 0.1716$$$$\text{大きな境界ボックス損失} = (\sqrt{w} - \sqrt{\hat{w}})^2 = (\sqrt{200} - \sqrt{300})^2 \approx 1.832$$

   平方根を使用することで、両者の損失差は大きく縮小します。この設計は、大きな境界ボックスが総損失に与える影響を過度に大きくしないようにするため、異なるサイズの境界ボックスに対してより公平な損失関数を作成するためのものです。

3. 信頼度損失（Confidence Loss）

   $$\sum_{i=0}^{S^2} \sum_{j=0}^{B} 1_{obj}^{ij} \left( C_i - \hat{C}_i \right)^2$$

   この部分の損失は、予測された境界ボックスが物体を含む信頼度（$C$）と真実の信頼度との違いを測定します。セル$i$と境界ボックス$j$が物体を含んでいる場合のみ、この損失が計算されます。

4. 非物体信頼度損失（No Object Confidence Loss）

   $$λ_{noobj} \sum_{i=0}^{S^2} \sum_{j=0}^{B} 1_{noobj}^{ij} \left( C_i - \hat{C}_i \right)^2$$

   この部分の損失は、予測された境界ボックスが物体を含まない信頼度と真実の信頼度との違いを測定します。ここでは、非物体の境界ボックスを過度に罰しないように、異なる重み係数$λ_{noobj}$が使用されています。

5. 分類損失（Class Probability Loss）

   $$\sum_{i=0}^{S^2} 1_{obj}^{i} \sum_{c \in \text{classes}} \left( p_i(c) - \hat{p}_i(c) \right)^2$$

   この部分の損失は、予測された分類確率$p_i(c)$と真実の分類確率との違いを測定します。セル$i$が物体を含む場合にのみ、この損失が計算されます。

推論シナリオ

各グリッドには 2 つの境界ボックスがあるため、毎回$S^2 \times B$個の境界ボックスが得られます。推論段階では、ここで非極大値抑制（Non-Maximum Suppression、NMS）を使用して、重複する境界ボックスをフィルタリングします。

非極大値抑制（NMS）は、物体検出アルゴリズム（YOLO や SSD など）の後処理技術であり、重複する候補ボックスをフィルタリングして、最も信頼度の高い境界ボックスを保持する方法です。

簡単に言うと、検出手順は以下の通りです：

1. 入力：一組の境界ボックスとそれに対応する信頼度スコア。
2. 並べ替え：信頼度スコアに基づいて境界ボックスを並べ替えます。
3. 選択：信頼度が最も高い境界ボックスを選択し、それを最終的に保持するボックスとして採用します。
4. 抑制：そのボックスと重なっている他の境界ボックスを、IoU（Intersection over Union）がある閾値を超えている場合に削除します。
5. 繰り返し：ステップ 3 とステップ 4 を繰り返し、すべてのボックスが処理されるまで続けます。

例を挙げると、以下の 4 つの検出ボックスがあり、それぞれの信頼度スコアと座標は次の通りです：

境界ボックス	信頼度	(x1, y1)	(x2, y2)
A	0.9	(10, 20)	(50, 60)
B	0.75	(12, 22)	(48, 58)
C	0.6	(15, 25)	(55, 65)
D	0.5	(60, 70)	(100, 110)

ステップ 1：並べ替え

信頼度スコアに基づいて境界ボックスを並べ替えます：

1. A (0.9)
2. B (0.75)
3. C (0.6)
4. D (0.5)

ステップ 2 と 3：選択と抑制

• 選択：信頼度が最も高い境界ボックス A を選択し、それを最終的に保持するボックスとして採用します。

• 抑制：A と重なっているボックス：

  • A と B の IoU を計算します。もし IoU > 閾値（例えば 0.5）であれば、B を削除します。
  • A と C の IoU を計算します。もし IoU > 閾値であれば、C を削除します。
  • A と D の IoU を計算します。A と D は重ならない（IoU = 0）ので、D を削除しません。

仮に、A と B の IoU が 0.7、A と C の IoU が 0.6 であり、いずれも閾値 0.5 を超えている場合、B と C は削除されます。

ステップ 3 と 4 の繰り返し

残りの境界ボックスは A と D です：

• 選択：次に信頼度が高い境界ボックス D を選択し、それを最終的に保持するボックスとして採用します。
• 抑制：他のボックスが残っていないため、このステップはスキップされます。

非極大値抑制を通じて、初期の 4 つの境界ボックスのうち、A と D の 2 つを保持し、重複した検出ボックスを効果的に排除しました。これにより、最も信頼度が高く、重複が最小限の境界ボックスだけが残り、検出結果の精度と信頼性が向上します。

討論

推論速度

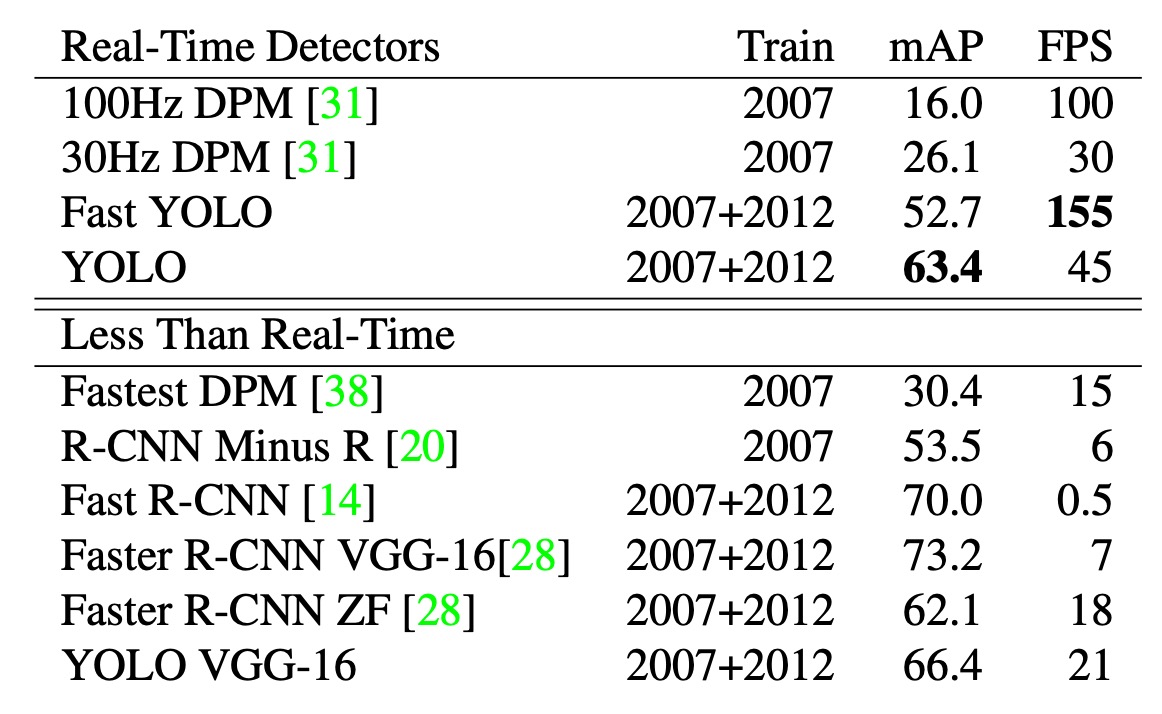
物体検出の分野では、検出プロセスの加速が多くの研究の重点となっています。上記の図は、PASCAL VOC 2007 における速度と精度の比較を示しています。

YOLO は、DPM の GPU 実装に比べて優れた性能を発揮し、30Hz または 100Hz で動作できます。Fast YOLO は PASCAL 上で最速の物体検出方法であり、52.7％の mAP を達成し、従来のリアルタイム検出精度を倍以上向上させました。

YOLO はさらに改善され、63.4％の mAP を達成し、依然としてリアルタイム性能を維持しています。VGG-16 を使用して訓練された YOLO モデルは精度が高いものの、速度が遅くなるため、本論文ではより高速なモデルに焦点を当てています。

それに対して、DPM はリアルタイム性能が 2 倍低下し、R-CNN および Fast R-CNN は依然としてリアルタイム要求を満たしておらず、Faster R-CNN は高い精度を持っていますが、速度は YOLO の 6 倍遅くなっています。

他の手法との比較

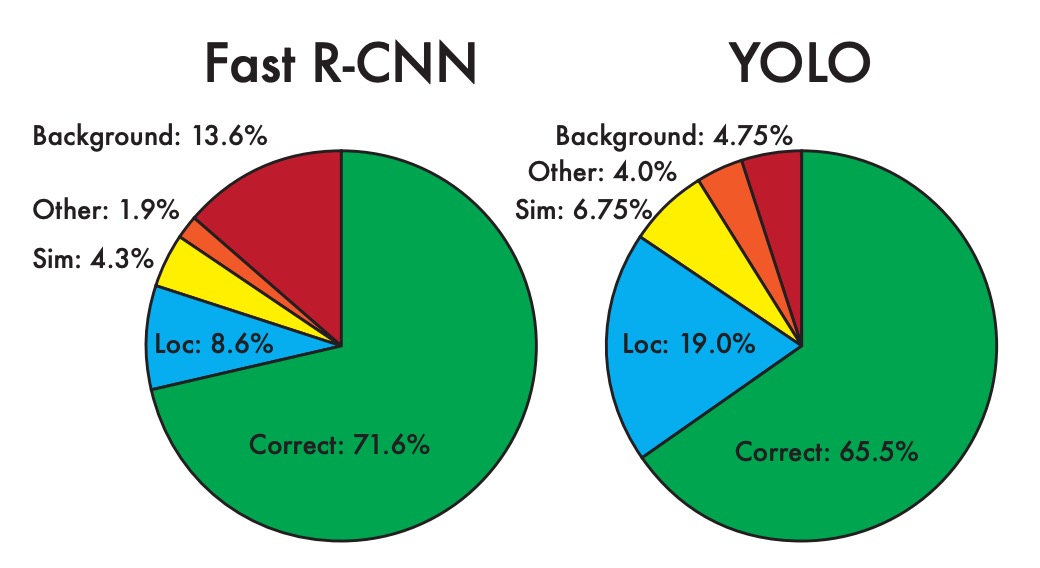
YOLO と最先端の検出器との違いをさらに調査するために、著者は VOC 2007 データセットで詳細な分類分析を行いました。このデータセットの検出結果は公開されています。

テストプロセスでは、各クラスの上位 N 個の予測を確認し、それぞれの予測を次のように分類しました：

• 正確（Correct）：正しいクラスで、IOU > 0.5
• 位置エラー（Localization）：正しいクラスで、IOU が 0.1 から 0.5 の間
• 類似（Similar）：類似するクラスで、IOU > 0.1
• その他（Other）：クラスが間違っているが、IOU > 0.1
• 背景（Background）：いかなる物体の IOU < 0.1

上の図は、全 20 クラスの各誤分類タイプの平均分布を示しています。

• 著者は、YOLO が物体を正確に位置付けることに難しさがあることを発見しました。

YOLO の誤差の中で、位置エラーの割合は他のすべての誤差タイプを合わせたよりも高くなっています。それに対して、Fast R-CNN は位置エラーが顕著に少ないですが、背景エラーが多くなっています。実験結果は、Fast R-CNN の 13.6％のトップ検出が物体を含まない誤報であり、その背景検出の誤報率は YOLO の約 3 倍であることを示しています。

YOLO は高速な検出において優れている一方で、物体を正確に位置付けることに課題があります。Fast R-CNN は位置付けが得意ですが、背景を物体として誤検出しやすいです。これにより、両者は精度や誤分類タイプにおいて異なる特徴を持ち、それぞれの利点と欠点が浮き彫りになっています。

モデルの制限

YOLO は境界ボックスの予測に強い空間的制約を課しており、各グリッドセルは 2 つのボックスしか予測できず、1 つのクラスしか扱えません。この空間的制限により、モデルが予測できる隣接する物体の数が制限されています。

著者は、モデルが小さな物体が群れをなして現れる場合（例えば鳥の群れ）に困難を抱えることを指摘しています。モデルはデータから境界ボックスを予測する方法を学習するため、新しいまたは異常なアスペクト比や構成の物体に対して汎用化するのが難しくなります。

さらに、YOLO は境界ボックスを予測するために比較的粗い特徴を使用しています。その理由は、アーキテクチャが入力画像を複数回ダウンサンプリングしているためです。これにより、特に小さな物体の予測において、境界ボックスの詳細な処理が不足する可能性があります。

著者はまた、YOLO の損失関数が小さな境界ボックスと大きな境界ボックスの誤差を同じように処理する点についても触れています。大きな境界ボックスの小さな誤差は影響が小さいですが、小さな境界ボックスの小さな誤差は IOU に与える影響が大きいため、最終的にモデルが物体を正確に位置付けるのが難しくなる原因となります。

結論

YOLO は革新的な物体検出方法であり、検出問題を単一の回帰問題として定義し、画像ピクセルから直接境界ボックスとクラス確率を予測することにより、エンドツーエンドの最適化を実現しました。

この統一モデルは、検出速度を大幅に向上させ、ベースとなる YOLO モデルは 1 秒あたり 45 フレームの速度でリアルタイムに画像を処理でき、精度においても優れた性能を示します。

小さな物体の精密な位置付けにはいくつかの課題があるものの、YOLO は多くの検出タスクで優れた汎用能力を発揮しており、今後のリアルタイム検出技術の発展に向けて堅実な基盤を築いています。