[20.01] Scaling Laws

Scaling Laws for Neural Language Models

Scaling Laws for Neural Language Models

---

OpenAI has been pushing the boundaries with the Transformer decoder architecture.

Problem Definition

From previous articles, you might have noticed OpenAI's ambition: they aim to build a "super-large" language model.

Thus, this study addresses a fundamental question:

• How exactly should one scale up a model?

This question is the core challenge this paper aims to solve.

Solution

In this paper, the following hyperparameters are used to parameterize the Transformer architecture:

• The dimension of the feed-forward layer
• The dimension of the attention output
• The number of attention heads per layer
• The number of layers: The depth of the Transformer
• The number of tokens: The context length, typically set to 1024

Training Process

Unless otherwise specified, the models are trained using the Adam optimizer for $2.5\times10^{5}$ steps, with a batch size of 512 sequences, each containing 1024 tokens. Due to memory limitations, models with more than 1 billion parameters use Adafactor for training.

Various learning rates and learning rate schedules were tested, and it was found that the results at convergence are generally unaffected by the learning rate schedule. Unless otherwise specified, all training uses a learning rate schedule with a linear warm-up for the first 3000 steps, followed by a gradual decay to zero.

Dataset

The models are trained on an "extended version of the WebText dataset."

• The original WebText dataset is derived from outbound links on Reddit that received at least three upvotes by December 2017.
• WebText2 includes outbound links from Reddit from January to October 2018, also requiring at least three upvotes.
• The text from these links was extracted using the Newspaper3k Python library, resulting in a dataset containing 20.3 million documents, totaling 96GB of text and $1.62\times10^{10}$ words.
• Byte-pair encoding (BPE) was applied for tokenization, yielding $2.29\times10^{10}$ tokens, with $6.6\times10^{8}$ tokens reserved for the test set.
• The models were evaluated on Books Corpus, Common Crawl, English Wikipedia, and other publicly available online book samples.

Variation Factors

To comprehensively study the scaling characteristics of language models, this paper conducted extensive model training with variations in the following aspects:

• Model size: Models ranging from 768 to 1.5 billion non-embedding parameters
• Dataset size: Datasets ranging from 22 million to 23 billion tokens
• Model shape: Including depth, width, number of attention heads, and feed-forward layer dimensions
• Context length: Most training uses a context length of 1024, but shorter contexts were also tested
• Batch size: Most training uses a batch size of $2^{19}$ tokens, but batch sizes were varied to measure the critical batch size

These experimental designs aim to systematically investigate the performance of models under different conditions and derive relevant scaling laws.

Discussion

Size Matters Most

Model performance largely depends on scale, with a weaker dependency on model shape. Model performance depends significantly on scale, which is composed of three factors:

1. N: Number of model parameters
2. D: Dataset size
3. C: Amount of computation used

Experiments indicate that within a reasonable range, performance dependency on other architectural hyperparameters (such as depth and width) is minimal.

Power Laws

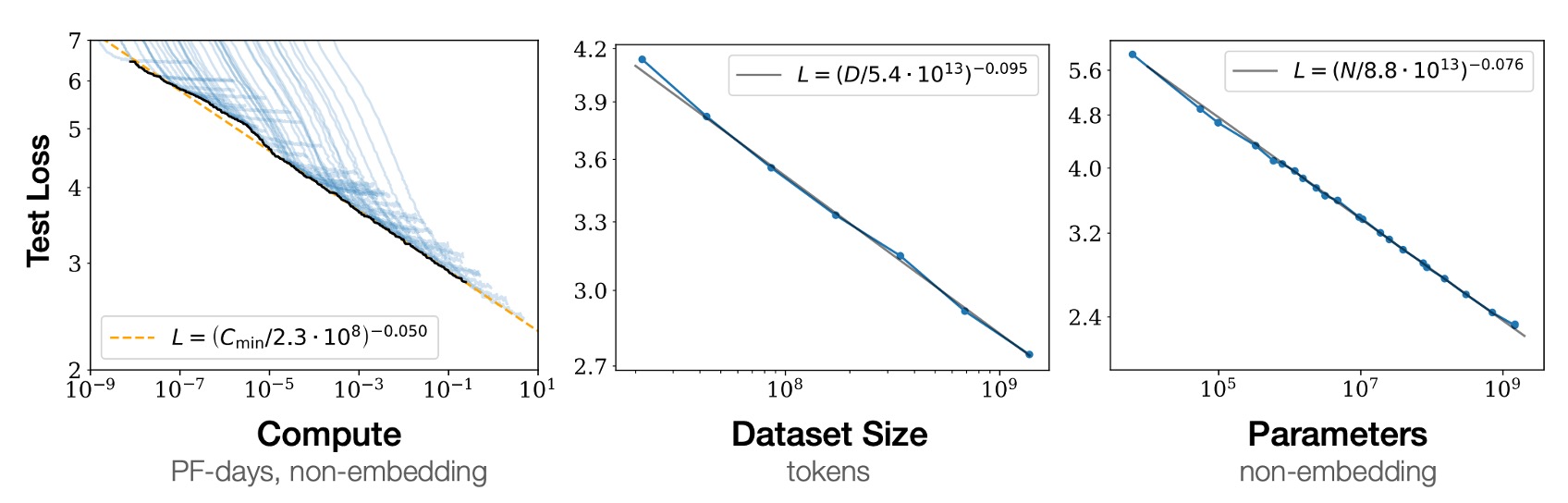
When not limited by the other two scaling factors, performance exhibits a power-law relationship with each of the three factors N, D, and C, spanning over "six orders of magnitude," as shown above.

• Left chart: More computation results in better model performance.
• Middle chart: Larger datasets yield better model performance.
• Right chart: More model parameters lead to better model performance.

tip

You might think this sounds obvious.

But it’s not. In past architectures, such as CNNs or LSTMs, these relationships didn't always hold. Performance could saturate or overfit. This cross-scaling relationship over six orders of magnitude is indeed a significant breakthrough.

The Universality of Overfitting

Experiments indicate that as long as we scale up N and D simultaneously, performance predictably improves. However, if N or D is held constant while the other increases, diminishing returns set in. The performance loss predictably depends on the ratio $N^{0.74}/D$, meaning every time we increase the model size by 8x, we only need to increase the data by about 5x to avoid loss.

Test Performance vs. Downstream Performance

Experiments indicate that when evaluating models on different texts from the distribution used for training, results are closely correlated with those on the training validation set, with a roughly constant offset in loss.

In other words, transitioning to a different distribution imposes a consistent penalty but otherwise scales with test performance.

Sample Efficiency

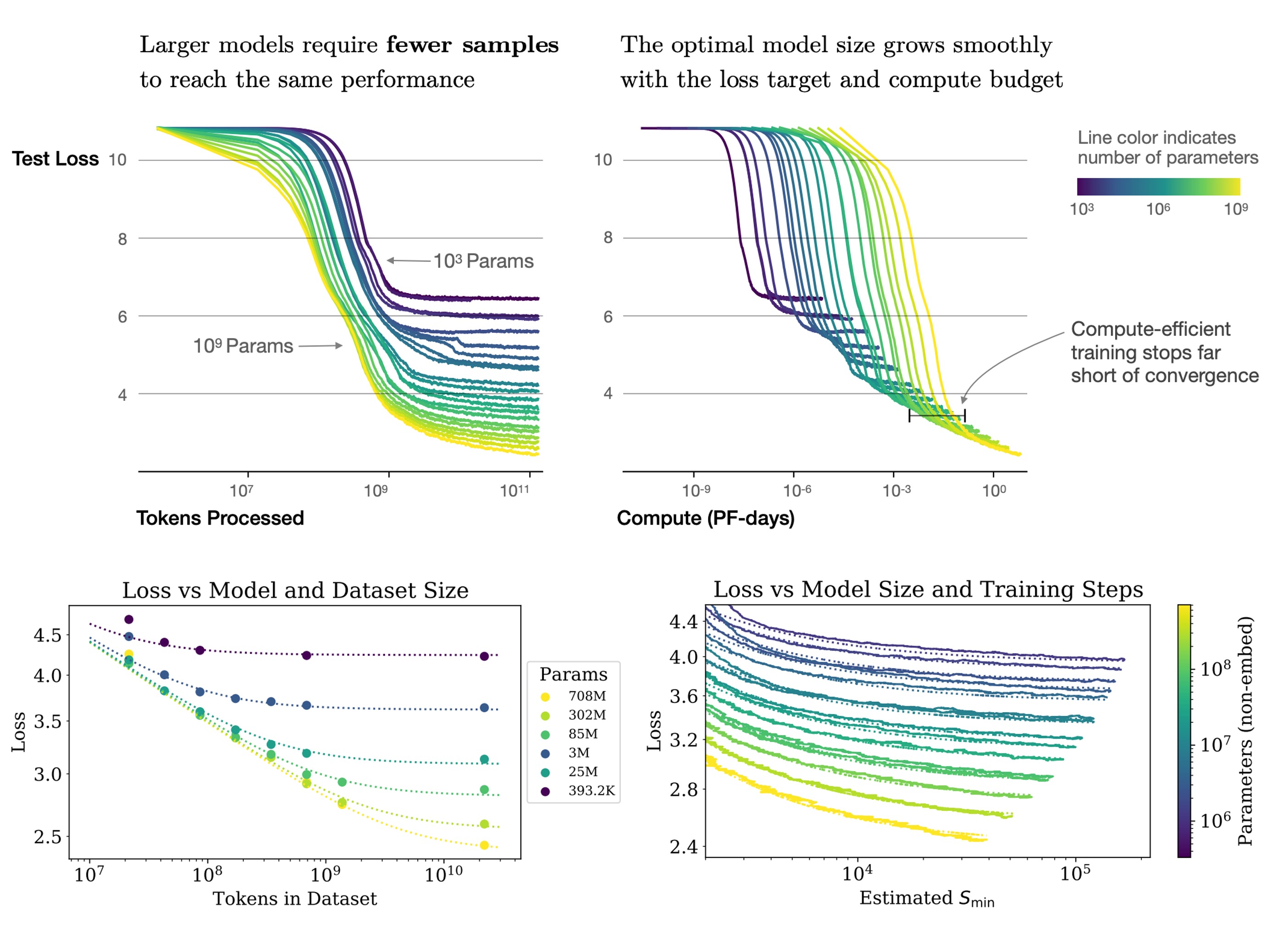
Larger models are more sample efficient than smaller ones, achieving the same level of performance with fewer optimization steps (first chart above) and using fewer data points (second chart above).

Convergence is Inefficient

As shown above, scaling up model size is a more efficient method than training smaller models to full convergence.

In simple terms, if we have fixed computational resources, it’s best to train very large models and stop them before they fully converge. This allows for the best performance within fixed computational budgets. Conversely, training smaller models to full convergence is less efficient.

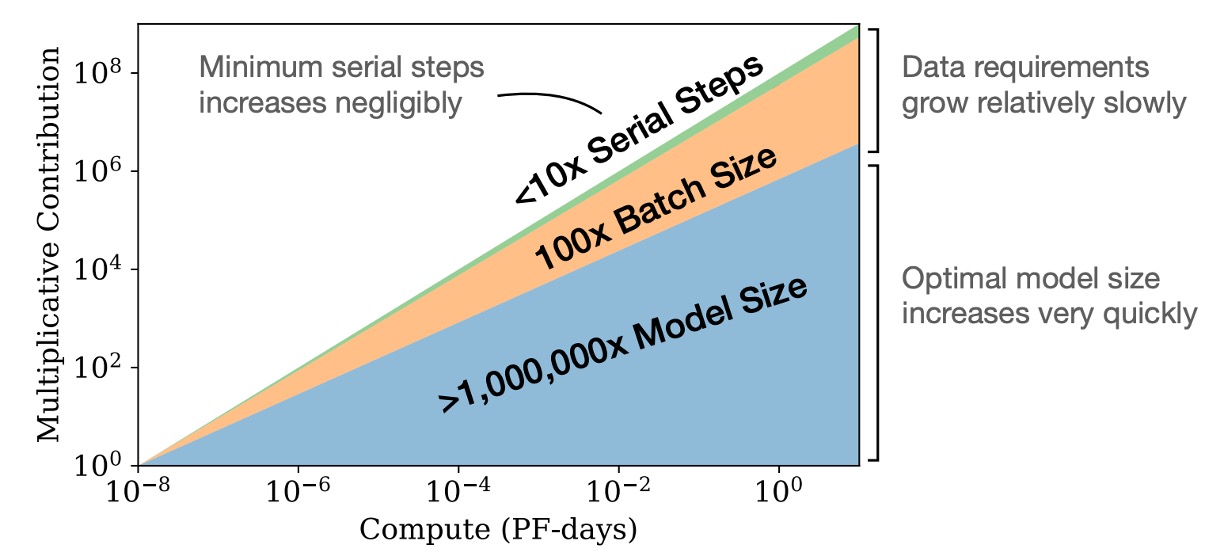
Additionally, as computational resources increase, the required training data increases slowly, so we don't need to massively increase data to match the increased computational resources.

Optimal Batch Size

The optimal batch size for training language models is not fixed but related to the loss function and can be determined by measuring the gradient noise scale.

In this paper, the largest model defined was 1.5 billion (1.5B) parameters. At optimal performance, the optimal batch size was around 1 to 2 million tokens. Such a batch size helps achieve optimal performance and effectiveness during training.

tip

The mentioned 1 to 2 million refers to the number of tokens, not the number of batch sizes. If the model's context length is 1024, the corresponding batch size would be around 1000 to 2000, achieving optimal results.

Conclusion

This paper conducted extensive experiments and summarized the training methods for language models.

To us, these conclusions are represented by large sums of money, and we gratefully accept these experimental results.